题目内容
命题p:实数x满足x2-4ax+3a2<0(其中a>0);命题q:实数x满足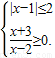
(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
【答案】分析:(I)将a=1代入,求出命题p为真时,x的范围;进而解不等式组求命题q为真时,x的范围,由p∧q为真,两个命题均为真,构造不等式组,即可得到实数x的取值范围;
(Ⅱ)¬p是¬q的充分不必要条件,则¬p⇒¬q,且¬q?¬p,根据(I)中结论,构造关于a的不等式,解得实数a的取值范围
解答:解:(Ⅰ)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
又a>0,所以a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.(2分)
由
得
解得2<x≤3,
即q为真时实数x的取值范围是2<x≤3.(4分)
若p∧q为真,则p真且q真,
所以实数x的取值范围是(2,3).(6分)
(Ⅱ)由(Ⅰ)知p:a<x<3a,
则¬p:x≤a或x≥3a,(8分)
q:2<x≤3,则¬q:x≤2或x>3,(10分)
¬p是¬q的充分不必要条件,则¬p⇒¬q,且¬q?¬p,
∴
解得1<a≤2,
故实数a的取值范围是(1,2].(12分)
点评:本题考查的知识点是命题的真假判断,充要条件,其中根据复合命题的真值表及充要条件的定义,将问题转化为不等式组,或集合关系问题是解答的关键.
(Ⅱ)¬p是¬q的充分不必要条件,则¬p⇒¬q,且¬q?¬p,根据(I)中结论,构造关于a的不等式,解得实数a的取值范围
解答:解:(Ⅰ)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
又a>0,所以a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.(2分)
由

得

解得2<x≤3,
即q为真时实数x的取值范围是2<x≤3.(4分)
若p∧q为真,则p真且q真,
所以实数x的取值范围是(2,3).(6分)
(Ⅱ)由(Ⅰ)知p:a<x<3a,
则¬p:x≤a或x≥3a,(8分)
q:2<x≤3,则¬q:x≤2或x>3,(10分)
¬p是¬q的充分不必要条件,则¬p⇒¬q,且¬q?¬p,
∴

解得1<a≤2,
故实数a的取值范围是(1,2].(12分)
点评:本题考查的知识点是命题的真假判断,充要条件,其中根据复合命题的真值表及充要条件的定义,将问题转化为不等式组,或集合关系问题是解答的关键.

练习册系列答案
相关题目
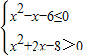 .
.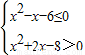 .
.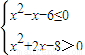 .
.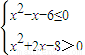 .
.