Question

正方形ABCD的两对角线AC与BD交于O，沿对角线BD折起，使∠AOC=90°对于下列结论：①AC⊥BD；②△ADC是正三角形；③AB与CD成60°角；④AB与平面BCD成60°角，其中正确的结论是    ．

Answer 1

【答案】分析：由正方体的几何特征，可得BD⊥平面AOC，根据线面垂直的性质定理，可判断①的真假；由三余弦定理，求出∠ADC的余弦值，我们可以确定∠ADC的大小，进而判断出△ADC的形状，判断出②③的真假，根据线面夹角的定理，我们易得∠ABO即为AB与平面BCD成角，求出∠ABO的大小，可以判断④的真假，进而得到答案．
解答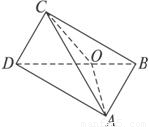： 解：由正方形的几何特征可得：
BD⊥OC，BD⊥OA，得BD⊥平面AOC，
故BD⊥AC，故①正确；
cos∠ADC=cos45°•cos45°=，
∴∠ADC=60°，AD=DC，
△ADC是正三角形，故②正确；
由②中结论可得，AB与CD成60°角，故③正确；
而AB与平面BCD成角∠ABO=45°，故④错误
故答案为：①②③
点评：本题考查的知识点是平面与平面垂直的性质，直线与平面所成的角，三角形形状的判断，异面直线的夹角，其中熟练掌握空间中直线与平面夹角及平行、垂直关系的定义、判定、性质和几何特征是解答本题的关键．