题目内容
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.(Ⅰ)求证:EF⊥平面BCD;
(Ⅱ)求二面角C-DE-A的大小.

【答案】分析:(Ⅰ)取BC中点G点,连接AG,FG,可证四边形EFGA为平行四边形,AE⊥平面ABC,AE∥BD,可证得BD⊥平面ABC,
继而可证得AG⊥平面BCD,由线面垂直的性质即可证得EF⊥平面BCD;
(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,设AB=2a,可求得C、D、E、A的坐标,从而可求得 =(-
=(- a,a,2a),
a,a,2a),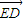 =(0,2a,a),设面CDE的法向量
=(0,2a,a),设面CDE的法向量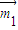 =(x,y,z),由
=(x,y,z),由 可取得
可取得 =(
=( ,-1,2),取面ABDE的法向量
,-1,2),取面ABDE的法向量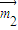 =(1,0,0),利用向量的夹角公式即可求得面角C-DE-A的大小.
=(1,0,0),利用向量的夹角公式即可求得面角C-DE-A的大小.
解答: 证明:(Ⅰ)取BC中点G点,连接AG,FG,
证明:(Ⅰ)取BC中点G点,连接AG,FG,
∵F,G分别为DC,BC中点,
∴FG∥BD且FG= BD,又AE∥BD且AE=
BD,又AE∥BD且AE= BD,
BD,
∴AE∥FG且AE=FG,
∴四边形EFGA为平行四边形,
∴EF∥AG,
∵AE⊥平面ABC,AE∥BD,
∴BD⊥平面ABC,
又∵DB?平面BCD,
∴平面ABC⊥平面BCD,
∵G为 BC中点,且AC=AB,
∴AG⊥BC,
∴AG⊥平面BCD,
∴EF⊥平面BCD.(6分)
(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,设AB=2a,则C(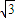 a,0,0),D(0,a,2a),E(0,-a,a),A(0,-a,0),
a,0,0),D(0,a,2a),E(0,-a,a),A(0,-a,0),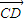 =(-
=(-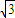 a,a,2a),
a,a,2a),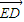 =(0,2a,a).
=(0,2a,a).
设面CDE的法向量 =(x,y,z),则
=(x,y,z),则
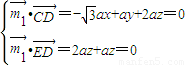 取
取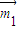 =(
=(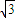 ,-1,2),(8分)
,-1,2),(8分)
取面ABDE的法向量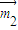 =(1,0,0),(10分)
=(1,0,0),(10分)
由cos< ,
,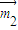 >=
>= =
= =
= ,
,
故二面角C-DE-A的大小为arccos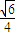 .(12分)
.(12分)
点评:本体考查直线与平面垂直的判定,考查二面角的平面角及求法,突出考查线与平面垂直的判定与性质的综合应用,考查向量法解决立体几何问题,考查综合分析与运算能力,属于难题.
继而可证得AG⊥平面BCD,由线面垂直的性质即可证得EF⊥平面BCD;
(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,设AB=2a,可求得C、D、E、A的坐标,从而可求得
 =(-
=(- a,a,2a),
a,a,2a),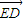 =(0,2a,a),设面CDE的法向量
=(0,2a,a),设面CDE的法向量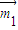 =(x,y,z),由
=(x,y,z),由 可取得
可取得 =(
=( ,-1,2),取面ABDE的法向量
,-1,2),取面ABDE的法向量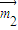 =(1,0,0),利用向量的夹角公式即可求得面角C-DE-A的大小.
=(1,0,0),利用向量的夹角公式即可求得面角C-DE-A的大小.解答:
 证明:(Ⅰ)取BC中点G点,连接AG,FG,
证明:(Ⅰ)取BC中点G点,连接AG,FG,∵F,G分别为DC,BC中点,
∴FG∥BD且FG=
 BD,又AE∥BD且AE=
BD,又AE∥BD且AE= BD,
BD,∴AE∥FG且AE=FG,
∴四边形EFGA为平行四边形,
∴EF∥AG,
∵AE⊥平面ABC,AE∥BD,
∴BD⊥平面ABC,
又∵DB?平面BCD,
∴平面ABC⊥平面BCD,
∵G为 BC中点,且AC=AB,
∴AG⊥BC,
∴AG⊥平面BCD,
∴EF⊥平面BCD.(6分)
(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,设AB=2a,则C(
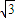 a,0,0),D(0,a,2a),E(0,-a,a),A(0,-a,0),
a,0,0),D(0,a,2a),E(0,-a,a),A(0,-a,0),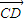 =(-
=(-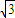 a,a,2a),
a,a,2a),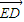 =(0,2a,a).
=(0,2a,a).设面CDE的法向量
 =(x,y,z),则
=(x,y,z),则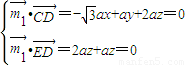 取
取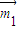 =(
=(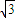 ,-1,2),(8分)
,-1,2),(8分)取面ABDE的法向量
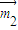 =(1,0,0),(10分)
=(1,0,0),(10分)由cos<
 ,
,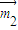 >=
>=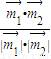 =
= =
= ,
,故二面角C-DE-A的大小为arccos
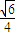 .(12分)
.(12分)点评:本体考查直线与平面垂直的判定,考查二面角的平面角及求法,突出考查线与平面垂直的判定与性质的综合应用,考查向量法解决立体几何问题,考查综合分析与运算能力,属于难题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 (2012•资阳二模)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.
(2012•资阳二模)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点. (2012•成都模拟)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
(2012•成都模拟)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
