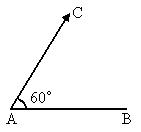
题目内容
甲乙两个滑冰者位于冰面上的A、B两点,A与B相距100米.如果甲从A出发,以8米/秒的速度与AB成60°角的直线滑行,同时乙以7米/秒的速度沿着与甲相遇的最短直线滑行,那么在相遇时,甲滑行了分析:假设甲乙在点C出相遇,设AC=8x,则 BC=7x,△ABC中,有余弦定理可得 49x2=64x2+10000-1600x•
,解出 x值,即得AC.
| 1 |
| 2 |
解答:解:假设甲乙在点C出相遇,设AC=8x,则 BC=7x,∠BAC=60°.
△ABC中,有余弦定理可得 BC2=AC2+AB2-2AC•AB•cos∠BAC,即
49x2=64x2+10000-1600x•
,∴x=20,∴AC=8x=160 (米),
故答案为 160米.
△ABC中,有余弦定理可得 BC2=AC2+AB2-2AC•AB•cos∠BAC,即
49x2=64x2+10000-1600x•
| 1 |
| 2 |
故答案为 160米.
点评:本题考查余弦定理得应用,设出AC=8x,则 BC=7x,是解题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
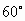 角的直线滑行,同时乙以7m/s的速度沿着与甲相遇的最短直线滑行,那么在相遇时,甲滑行了多远?
角的直线滑行,同时乙以7m/s的速度沿着与甲相遇的最短直线滑行,那么在相遇时,甲滑行了多远?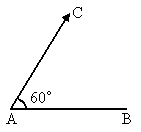
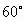 角的直线滑行,同时乙以7m/s的速度沿着与甲相遇的最短直线滑行,那么在相遇时,甲滑行了多远?
角的直线滑行,同时乙以7m/s的速度沿着与甲相遇的最短直线滑行,那么在相遇时,甲滑行了多远?