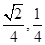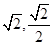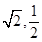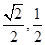题目内容
已知函数 是周期为2的周期函数,且当
是周期为2的周期函数,且当 时,
时,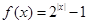 ,则函数
,则函数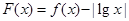 的零点个数是( )
的零点个数是( )
| A.9 | B.10 | C.11 | D.12 |
B
解析试题分析:由于函数 是周期为2的周期函数,所以
是周期为2的周期函数,所以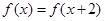 .因为
.因为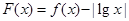 的零点个数等价于
的零点个数等价于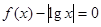 方程的根的个数.即函数
方程的根的个数.即函数 与函数
与函数 的个数.又
的个数.又 时,
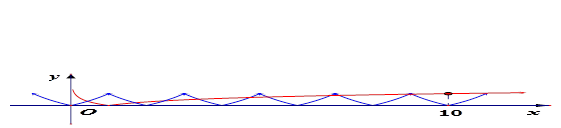
时,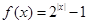 .如图所示.共有10个交点,即选B.
.如图所示.共有10个交点,即选B.
考点:1.函数的周期性.2.函数与方程的关系.3.对数指数函数的图象.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列函数中,在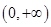 上单调递减,并且是偶函数的是( )
上单调递减,并且是偶函数的是( )
A.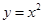 | B.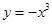 | C.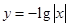 | D.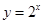 |
函数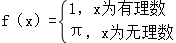 ,下列结论不正确的( )
,下列结论不正确的( )
| A.此函数为偶函数 |
| B.此函数是周期函数 |
| C.此函数既有最大值也有最小值 |
| D.方程f[f(x)]=1的解为x=1 |
函数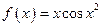 在区间[0,4]上的零点个数为( )
在区间[0,4]上的零点个数为( )
| A.4 | B.5 | C.6 | D.7 |
函数f(x)=2x2-lnx的单调递增区间是( )
A. |
B.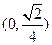 |
C.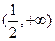 |
D.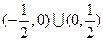 |
函数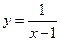 的图像与函数
的图像与函数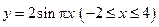 的图像所有交点的横坐标之和等于( )
的图像所有交点的横坐标之和等于( )
| A.2 |
| B.4 |
| C.6 |
| D.8 |
 是周期为2的周期函数,且当
是周期为2的周期函数,且当 时,
时,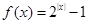 ,则函数
,则函数 的零点个数是( )
的零点个数是( )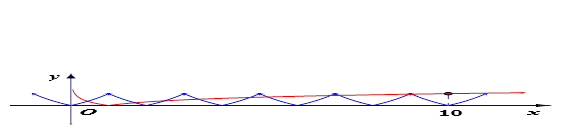
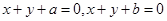 ,已知
,已知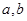 是方程
是方程 的两个实根,且
的两个实根,且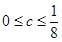 ,则这两条直线之间的距离的最大值和最小值分别是( )
,则这两条直线之间的距离的最大值和最小值分别是( )