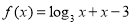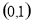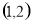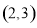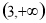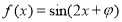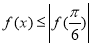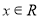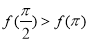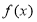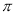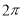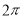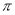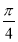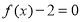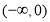题目内容
已知函数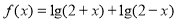 .
.
(Ⅰ)求函数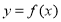 的定义域;
的定义域;
(Ⅱ)判断函数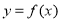 的奇偶性;
的奇偶性;
(Ⅲ)若 ,求
,求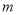 的取值范围.
的取值范围.
(1)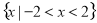 ;(2)偶函数;(3)
;(2)偶函数;(3)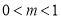 .
.
【解析】
试题分析:(1)由对数函数的真数大小零的要求即可得到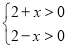 ,从中求解可求出函数的定义域;(2)先判断定义域关于原点对称,再根据定义:若
,从中求解可求出函数的定义域;(2)先判断定义域关于原点对称,再根据定义:若 ,则函数
,则函数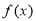 为偶函数,若
为偶函数,若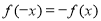 ,则函数
,则函数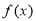 为奇函数;(3)由复合函数的单调性先判断函数
为奇函数;(3)由复合函数的单调性先判断函数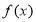 在
在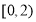 单调递减,再结合
单调递减,再结合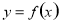 为偶函数的条件,可将不等式
为偶函数的条件,可将不等式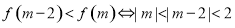 ,然后进行求解可得
,然后进行求解可得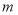 的取值范围.
的取值范围.
试题解析:(Ⅰ)要使函数有意义,则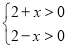 ,得
,得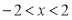 3分
3分
 函数
函数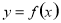 的定义域为
的定义域为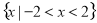 5分
5分
(Ⅱ)由(Ⅰ)可知,函数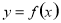 的定义域为
的定义域为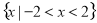 ,关于原点对称,对任意
,关于原点对称,对任意 ,
,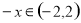
 8分
8分
 由函数奇偶性可知,函数
由函数奇偶性可知,函数 为偶函数 10分
为偶函数 10分
(Ⅲ)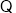 函数
函数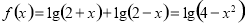
由复合函数单调性判断法则知,当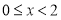 时,函数
时,函数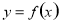 为减函数
为减函数
又函数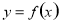 为偶函数,
为偶函数, 不等式
不等式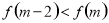 等价于
等价于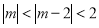 , 13分
, 13分
得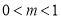 15分.
15分.
考点:1.函数的定义域;2.对数函数;3.函数的奇偶性;4.复合函数的单调性.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目