题目内容
已知函数![]() =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若y=f(x)在[-1,1]上存在零点,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).解析:(Ⅰ):因为函数![]() =x2-4x+a+3的对称轴是x=2,
=x2-4x+a+3的对称轴是x=2,
所以![]() 在区间[-1,1]上是减函数,
在区间[-1,1]上是减函数,
因为函数在区间[-1,1]上存在零点,则必有:
![]() 即
即![]() ,解得
,解得![]() ,
,
故所求实数a的取值范围为[-8,0] .
(Ⅱ)若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,只需函数y=f(x)的值域为函数y=g(x)的值域的子集.
![]() =x2-4x+3,x∈[1,4]的值域为[-1,3],下求g(x)=mx+5-2m的值域.
=x2-4x+3,x∈[1,4]的值域为[-1,3],下求g(x)=mx+5-2m的值域.
①当m=0时,g(x)=5-2m为常数,不符合题意舍去;
②当m>0时,g(x)的值域为[5-m,5+2m],要使[-1,3]![]() [5-m,5+2m],
[5-m,5+2m],
需![]() ,解得m≥6;
,解得m≥6;
③当m<0时,g(x)的值域为[5+2m,5-m],要使[-1,3]![]() [5+2m,5-m],
[5+2m,5-m],
需![]() ,解得m≤-3;
,解得m≤-3;
综上,m的取值范围为![]() .
.
(Ⅲ)由题意知![]() ,可得
,可得![]() .
.
①当t≤0时,在区间[t,4]上,f(t)最大,f(2)最小,
所以f(t)-f(2)=7-2 t即t2-2t-3=0,解得t=-1或t=3(舍去);
②当0<t≤2时,在区间[t,4]上,f(4)最大,f(2)最小,
所以f(4)-f(2)=7-2 t即4=7-2t,解得t=![]() ;
;
③当2<t<![]() 时,在区间[t,4]上,f(4)最大,f(t)最小,
时,在区间[t,4]上,f(4)最大,f(t)最小,
所以f(4)-f(t)=7-2t即t2-6t+7=0,解得t=![]() (舍去)
(舍去)

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
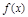 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m. =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.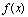 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.