题目内容
下列命题:
①若 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数, ,
,
则
②在 中,
中, 是
是 的充要条件.
的充要条件.
③若 为非零向量,且
为非零向量,且 ,则
,则 .
.
④在△ABC中,角A、B、C所对的边分别为a,b,c,已知b2 + c2
= a2 + bc,则
其中真命题的个数有 ( )
A.1 B.2 C.3 D.4
【答案】
B
【解析】
试题分析:
①由已知可得函数在[0,1]上为减函数,∵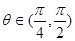 ∴1>sinθ>cosθ>0,∴f(sinθ)<f(cosθ),故①错;
∴1>sinθ>cosθ>0,∴f(sinθ)<f(cosθ),故①错;
②∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),
∵在(0,π)上,y=cosx是减函数,∴△ABC中,“A>B”?“cosA<cosB”,故②正确;
③因为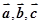 为非零向量,且
为非零向量,且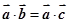 ,则
,则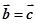 .向量没有除法运算,故错误。
.向量没有除法运算,故错误。
④∵b2+c2=a2+bc,∴a2=b2+c2-bc,
结合余弦定理知cosA=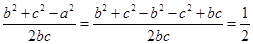 ,
,
又A∈(0,π),∴A=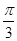 ,故④正确.从而真命题的个数有两个,故选B
,故④正确.从而真命题的个数有两个,故选B
考点:命题真假的判定以及充要条件
点评:本题的考点是命题的真假判断与应用,解题时需依据函数的性质,余弦定理一一判断,综合性强.

练习册系列答案
相关题目