题目内容
设 是奇函数,则使f(x)<0的x的取值范围是( )
是奇函数,则使f(x)<0的x的取值范围是( )A.(-1,0)
B.(0,1)
C.(-∞,0)
D.(-∞,0)∪(1,+∞)
【答案】分析:首先由奇函数定义,得到f(x)的解析式的关系式(本题可利用特殊值f(0)=0),求出a,
然后由对数函数的单调性解之.
解答:解:由f(-x)=-f(x),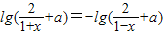 ,
,
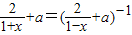 ,即
,即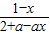 =
=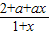 ,
,
1-x2=(2+a)2-a2x2
此式恒成立,可得a2=1且(a+2)2=1,所以a=-1
则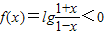
即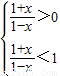
解得-1<x<0
故选A
点评:本题主要考查奇函数的定义,同时考查对数函数的单调性.
然后由对数函数的单调性解之.
解答:解:由f(-x)=-f(x),
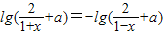 ,
,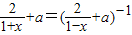 ,即
,即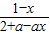 =
=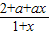 ,
,1-x2=(2+a)2-a2x2
此式恒成立,可得a2=1且(a+2)2=1,所以a=-1
则
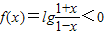
即
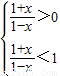
解得-1<x<0
故选A
点评:本题主要考查奇函数的定义,同时考查对数函数的单调性.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
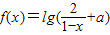 是奇函数,则使f(x)<0的x的取值范围是( )
是奇函数,则使f(x)<0的x的取值范围是( )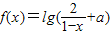 是奇函数,则使f(x)<0的x的取值范围是( )
是奇函数,则使f(x)<0的x的取值范围是( )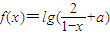 是奇函数,则使f(x)<0的x的取值范围是( )
是奇函数,则使f(x)<0的x的取值范围是( ) 是奇函数,则使f (x)<0成立的x的取值范围是__________
是奇函数,则使f (x)<0成立的x的取值范围是__________