题目内容
设l,m是两条异面直线,在l上有A,B,C三点,且AB=BC,过A,B,C分别作m的垂线AD,BE,CF,垂足依次是D,E,F,已知AD=
,BE=
CF=
,求l与m的距离.
| 15 |
| 7 |
| 2 |
| 10 |
分析:过m作平面α∥l,作AP⊥α于P,AP与l确定平面β,β∩α=l',l'∩m=K.作BQ⊥α,CR⊥α,垂足分别为Q、R,根据三垂线定理逆定理,得PD、QE、RF都垂直于m,设d为异面直线l、m的距离,得PD=
,QE=
,RF=
,最后根据点D、E、F与K的位置进行分类,建立方程并解之,即得异面直线l与m的距离.
| 15-d2 |
|
| 10-d2 |
解答:解:过m作平面α∥l,作AP⊥α于P,AP与l确定平面β,β∩α=l',l'∩m=K
作BQ⊥α,CR⊥α,垂足分别为Q、R,则Q、R∈l',且AP=BQ=CR=d,d为异面直线l、m的距离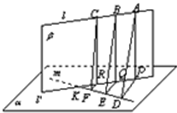
连接PD、QE、RF,则由三垂线定理逆定理,得
∵AD⊥m,BE⊥m,CF⊥m,PD、QE、RF分别为AD、BE、CF在α内的射影
∴PD、QE、RF都与直线m垂直,
∴PD=
,QE=
,RF=
当D、E、F在K的同侧时,2QE=PD+RF
∴
=
+
,解之得d=
当D、E、F在K的两侧时,2QE=PD-RF
∴
=
-
,解之得方程无实数根
综上所述,得异面直线l、m的距离d=
作BQ⊥α,CR⊥α,垂足分别为Q、R,则Q、R∈l',且AP=BQ=CR=d,d为异面直线l、m的距离

连接PD、QE、RF,则由三垂线定理逆定理,得
∵AD⊥m,BE⊥m,CF⊥m,PD、QE、RF分别为AD、BE、CF在α内的射影
∴PD、QE、RF都与直线m垂直,
∴PD=
| 15-d2 |
|
| 10-d2 |
当D、E、F在K的同侧时,2QE=PD+RF
∴
| 49-4d2 |
| 15-d2 |
| 10-d2 |
| 6 |
当D、E、F在K的两侧时,2QE=PD-RF
∴
| 49-4d2 |
| 15-d2 |
| 10-d2 |
综上所述,得异面直线l、m的距离d=
| 6 |
点评:本题给出两条异面直线,在已知一直线上等距离的三点到另一直线距离的情况下求两条异面直线的距离,着重考查了空间的垂直位置关系和异面直线距离求法等知识点,属于基础题.

练习册系列答案
相关题目