题目内容
若函数 的定义域为
的定义域为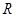 ,且存在常数
,且存在常数 ,对任意
,对任意 ,有
,有 ,则称
,则称 为
为 函数。给出下列函数:①
函数。给出下列函数:① ,②
,② ,③
,③ ,④
,④ 是定义在
是定义在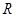 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数 均有
均有 ,⑤
,⑤ ,其中是
,其中是 函数的有____________________。
函数的有____________________。
【答案】
③④
【解析】对于①和⑤由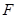 函数的定义得存在正实数m对任意x恒有
函数的定义得存在正实数m对任意x恒有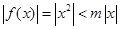 成立,显然当x=0时式子不成立,故①和⑤不是F函数;对于②由
成立,显然当x=0时式子不成立,故①和⑤不是F函数;对于②由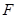 函数的定义得存在正实数m对任意x恒有
函数的定义得存在正实数m对任意x恒有 成立,作出
成立,作出 (m>0)的图象,发现函数
(m>0)的图象,发现函数 不全在函数
不全在函数 的图象下方,故②不是F函数;对于③④函数符合F函数的定义,故填③④
的图象下方,故②不是F函数;对于③④函数符合F函数的定义,故填③④

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域为
的定义域为 ,且
,且 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 .
. ,
, ,判断
,判断 ,并说明理由;
,并说明理由; 若
若 ,
,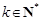 且
且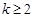 ,函数
,函数 .
. 的定义域为
的定义域为 ,且满足
,且满足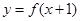 为 奇函数,
为 奇函数,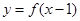 为偶函数,则下列说法中一定正确的有
为偶函数,则下列说法中一定正确的有  对称
对称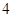

 上只有一个零点
上只有一个零点