题目内容
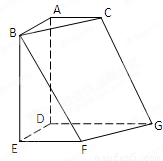
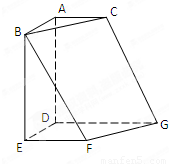
 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.(Ⅰ)求证:四点B、C、G、F共面;
(Ⅱ)求二面角D-BC-F的大小.
分析:(Ⅰ)设M是DG的中点,证明BF∥AM,AM∥CG,由此能得到四点B、C、G、F共面.
(Ⅱ)以DE为x轴,以DG为y轴,以DA为z轴,建立空间直角坐标系,利用向量法能求出二面角D-BC-F的大小.
(Ⅱ)以DE为x轴,以DG为y轴,以DA为z轴,建立空间直角坐标系,利用向量法能求出二面角D-BC-F的大小.
解答: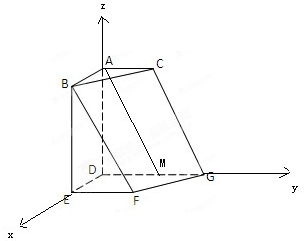 (Ⅰ)证明:取DG的中点M,连接AM,
(Ⅰ)证明:取DG的中点M,连接AM,
∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,
AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1
∴BF∥AM,AM∥CG,
∴BF∥CG,
∴四点B、C、G、F共面.
(Ⅱ)以DE为x轴,以DG为y轴,以DA为z轴,建立空间直角坐标系,
∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,
AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1
∴D(0,0,0),B(2,0,2),C(0,1,2)F(2,1,0),
∴
=(2,0,2),
=(0,1,2),
=(0,-1,2),
=(-2,0,2),
设平面DBC的法向量
=(x1,y1,z1),则
•
=0,
•
=0,
∴
,解得
=(1,2,-1),
设平面FBC的法向量
=(x2,y2,z2),则
•
=0,
•
=0,
∴
,解得
=(1,2,1),
设二面角D-BC-F的平面角为θ,
则cosθ=|cos<
,
>|=|
|=
.
∴二面角D-BC-F的大小为arccos
.
 (Ⅰ)证明:取DG的中点M,连接AM,
(Ⅰ)证明:取DG的中点M,连接AM,∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,
AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1
∴BF∥AM,AM∥CG,
∴BF∥CG,
∴四点B、C、G、F共面.
(Ⅱ)以DE为x轴,以DG为y轴,以DA为z轴,建立空间直角坐标系,
∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,
AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1
∴D(0,0,0),B(2,0,2),C(0,1,2)F(2,1,0),
∴
| DB |
| DC |
| FB |
| FC |
设平面DBC的法向量
| m |
| DB |
| m |
| DC |
| m |
∴
|
| m |
设平面FBC的法向量
| n |
| FB |
| n |
| FC |
| n |
∴
|
| n |
设二面角D-BC-F的平面角为θ,
则cosθ=|cos<
| m |
| n |
| 1+4-1 | ||||
|
| 2 |
| 3 |
∴二面角D-BC-F的大小为arccos
| 2 |
| 3 |
点评:本题考查四点共面的证明,考查二面角的求法.解题时要认真审题,注意平面的基本性质和向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
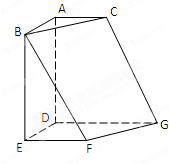 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.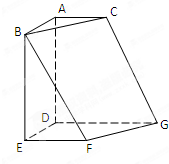 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.