题目内容
已知M是以点C为圆心的圆(x+1)2+y2=8上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足 .动点N的轨迹为曲线E.
.动点N的轨迹为曲线E.(Ⅰ)求曲线E的方程;
(Ⅱ)线段AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的取值范围.
【答案】分析:(Ⅰ)由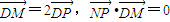 .知NP为DM的垂直平分线,所以|ND|=|NM|,动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为
.知NP为DM的垂直平分线,所以|ND|=|NM|,动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为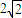 的椭圆.由此能求出轨迹E的方程.
的椭圆.由此能求出轨迹E的方程.
(Ⅱ)线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+b,由 ,得(1+2k2)x2+4kbx+2b2-2=0.设A(x1,y1),B(x2,y2),再由根与系数的关系进行求解.
,得(1+2k2)x2+4kbx+2b2-2=0.设A(x1,y1),B(x2,y2),再由根与系数的关系进行求解.
解答:解:(Ⅰ)∵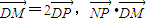 =0.
=0.
∴NP为DM的垂直平分线,∴|ND|=|NM|,
又∵|CN|+|NM|=2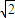 ,∴|CN|+|DN|=2
,∴|CN|+|DN|=2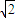 >2.(3分)
>2.(3分)
∴动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为2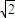 的椭圆.
的椭圆.
∴轨迹E的方程为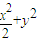 =1.(5分)
=1.(5分)
(Ⅱ)∵线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+b,
由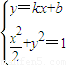 ,
,
消去y,并整理,得(1+2k2)x2+4kbx+2b2-2=0.
设A(x1,y1),B(x2,y2),
则x1+x2=-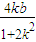 ,x1x2=
,x1x2=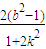 (8分)
(8分)
∵|AB|=2,∴ =2.
=2.
∴(1+k2)[(x1+x2)2-4x1x2]=4,
∴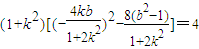 ,
,
∴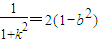 ,(11分)
,(11分)
∵1+k2≥1∴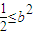 <1. (12分)
<1. (12分)
又点O到直线AB的距离h=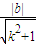 ,
,
∴S= |AB|•h=h
|AB|•h=h
∴S2=h2=2b2(1-b2)=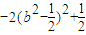 (13分)
(13分)
∴0<S2≤ ,∴0<S≤
,∴0<S≤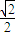 .(14分)
.(14分)
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.
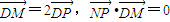 .知NP为DM的垂直平分线,所以|ND|=|NM|,动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为
.知NP为DM的垂直平分线,所以|ND|=|NM|,动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为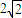 的椭圆.由此能求出轨迹E的方程.
的椭圆.由此能求出轨迹E的方程.(Ⅱ)线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+b,由
 ,得(1+2k2)x2+4kbx+2b2-2=0.设A(x1,y1),B(x2,y2),再由根与系数的关系进行求解.
,得(1+2k2)x2+4kbx+2b2-2=0.设A(x1,y1),B(x2,y2),再由根与系数的关系进行求解.解答:解:(Ⅰ)∵
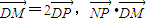 =0.
=0.∴NP为DM的垂直平分线,∴|ND|=|NM|,
又∵|CN|+|NM|=2
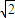 ,∴|CN|+|DN|=2
,∴|CN|+|DN|=2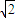 >2.(3分)
>2.(3分)∴动点N的轨迹是以点C(-1,0),D(1,0)为焦点的长轴为2
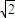 的椭圆.
的椭圆.∴轨迹E的方程为
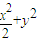 =1.(5分)
=1.(5分)(Ⅱ)∵线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+b,
由
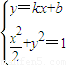 ,
,消去y,并整理,得(1+2k2)x2+4kbx+2b2-2=0.
设A(x1,y1),B(x2,y2),
则x1+x2=-
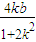 ,x1x2=
,x1x2=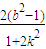 (8分)
(8分)∵|AB|=2,∴
 =2.
=2.∴(1+k2)[(x1+x2)2-4x1x2]=4,
∴
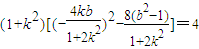 ,
,∴
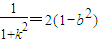 ,(11分)
,(11分)∵1+k2≥1∴
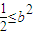 <1. (12分)
<1. (12分)又点O到直线AB的距离h=
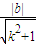 ,
,∴S=
 |AB|•h=h
|AB|•h=h∴S2=h2=2b2(1-b2)=
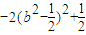 (13分)
(13分)∴0<S2≤
 ,∴0<S≤
,∴0<S≤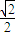 .(14分)
.(14分)点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
相关题目
 上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足
上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足 .动点
.动点 的轨迹为(***)
的轨迹为(***) .动点N的轨迹为曲线E.
.动点N的轨迹为曲线E.