题目内容
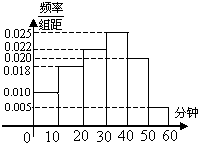
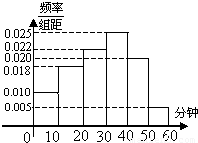
电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
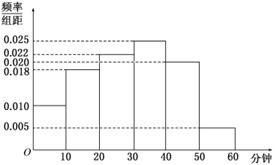
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
|
|
非体育迷 |
体育迷 |
合计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
合计 |
|
|
|
(Ⅱ)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2名,求至少有1名女性观众的概率.
附:K2=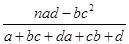 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
|
P(K2≥k) |
0.05 |
0.01 |
|
k |
3.841 |
6.635 |
(1) 没有95%的把握认为“体育迷”与性别有关(2) 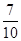
【解析】
试题分析:解: (Ⅰ)由频率分布直方图可知,在抽取的100名观众中,“体育迷”共25名,从而完成2×2列联表如下:
|
|
非体育迷 |
体育迷 |
合计 |
|
男 |
30 |
15 |
45 |
|
女 |
45 |
10 |
55 |
|
合计 |
75 |
25 |
100 |
2分
将2×2列联表中的数据代入公式计算,得
K2=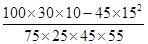 =
=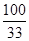 ≈3.030.
4分
≈3.030.
4分
因为3.030<3.841,所以我们没有95%的把握认为“体育迷”与性别有关. 6分
(Ⅱ)由频率分布直方图可知,“超级体育迷”有5名,从而一切可能结果所组成的基本事件空间为Ω={(a1,a2),(a1,a3),(a2,a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},其中ai表示男性,i=1,2,3;bj表示女性,j=1,2.
Ω由10个基本事件组成,而且这些基本事件的出现是等可能的. 8分
用A表示“任选2名,至少有1名是女性”这一事件,则
A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},事件A由7个基本事件组成, 10分 因而P(A)=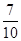 .
11分
.
11分
答:至少有1名女性观众的概率为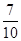 12分
12分
考点:本试题考查了古典概型和独立性检验的运用。
点评:对于古典概型的概率计算是一个重要的知识点,需要体会其总的试验空间以及事件发生的基本事件空间,然后利用比值来得到概率的值。而对于独立性检验主要是借助于观测值来分析把握的大小,属于基础题。

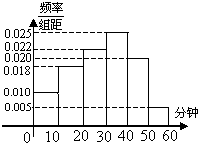 电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷“与性别有关?
电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷“与性别有关?