题目内容
设a,b是两个实数,且a≠b,① ②
② ,③
,③ 。上述三个式子恒成立的有( )
。上述三个式子恒成立的有( )
A.0个 B.1个 C.2个 D.3个
【答案】
B.
【解析】
试题分析:假设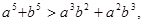 恒成立可得
恒成立可得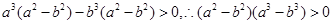 .即
.即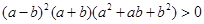 .因为
.因为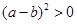 ,
,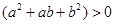 ,又因为
,又因为 的正负不能确定所以
的正负不能确定所以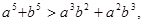 不能恒成立.
不能恒成立.
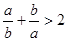 如果
如果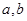 异号显然不成立.又有
异号显然不成立.又有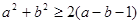 可化为
可化为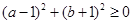 .该式显然成立.所以选B.本题考查不等式的性质,因式分解,基本不等式等知识的.第三个式子易判断错.强调基本不等式的“一正二定三相等”一项都不能少.
.该式显然成立.所以选B.本题考查不等式的性质,因式分解,基本不等式等知识的.第三个式子易判断错.强调基本不等式的“一正二定三相等”一项都不能少.
考点:1.因式分解.2.几个非负数的和大于等于零.3.基本不等式.

练习册系列答案
相关题目
 +b
+b