题目内容
利用三角函数线求满足下列条件的角α的集合.
(1)tanα=-1;(2)sinα<-
.
(1)tanα=-1;(2)sinα<-
| 1 | 2 |
分析:(1)作出过点(1,-1)和原点的直线交单位圆于P和P',然后在[0,2π)内找出满足条件tanα=-1的角α,再根据终边相同的角的集合,即可得到所有满足条件的角的集合;
(2)过点(0,-
)作x轴的平行线交单位圆于P和P',在[0,2π)内找出当
<x<
时,sinα<-
成立,再由终边相同的角的集合,即可得到所有满足条件的角的集合;
(2)过点(0,-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
| 1 |
| 2 |
解答:解:(1)如图①所示,过点(1,-1)和原点作直线交单位圆于P和P',
则射线OP、OP'就是满足tanα=-1的角α的终边
∵在[0,2π)内,满足条件的∠POx=π-
=
,∠P'Ox=-
∴满足条件tanα=-1的角α的集合是{x|x=-
+kπ,k∈Z}
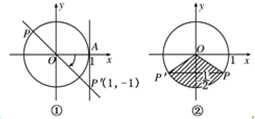
(2)如图②所示,过点(0,-
)作x轴的平行线,交单位圆于P和P',
则sin∠POx=sin∠P'Ox=-
∵在[0,2π)内,满足条件sinα=-
的∠P'Ox=
,∠POx=
观察图形可得:当
<x<
时,sinα<-
成立
∴满足条件sinα<-
的角α的集合是{x|
+2kπ<x<
+2kπ,k∈Z}
则射线OP、OP'就是满足tanα=-1的角α的终边
∵在[0,2π)内,满足条件的∠POx=π-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴满足条件tanα=-1的角α的集合是{x|x=-
| π |
| 4 |
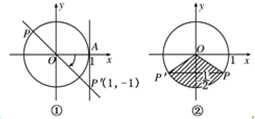
(2)如图②所示,过点(0,-
| 1 |
| 2 |
则sin∠POx=sin∠P'Ox=-
| 1 |
| 2 |
∵在[0,2π)内,满足条件sinα=-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
观察图形可得:当
| 7π |
| 6 |
| 11π |
| 6 |
| 1 |
| 2 |
∴满足条件sinα<-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
点评:本题给出满足条件的角,要求利用单位圆找出角α的集合.着重考查了单位圆中的三角函数线、终边相同角的集合等知识,属于基础题.

练习册系列答案
相关题目
 的角x的集合.
的角x的集合. 的角x的集合.
的角x的集合. .
.