题目内容
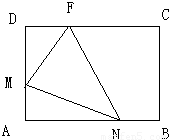
如图所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、BA的方向运动,当第二次MF=MN时M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,设动点M、N的速度都是1个单位/秒,M、N运动的时间为t秒.试解答下列问题:(1)求F、M、N三点共线时t的值;
(2)设△FMN的面积为S,写出S与t的函数关系式.并求出t为何值时S的值最大.
(3)试问t为何值时,△FMN为直角三角形?

【答案】分析:以A为坐标原点,AB,AD为x,y轴正方向建立坐标系,结合两点之间的距离公式,构造关于t的方程,解方程可得t的取值范围
(1)若F、M、N三点共线,则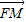 ∥
∥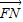 ,结合向量共线的充要条件,可求出满足条件的t值.
,结合向量共线的充要条件,可求出满足条件的t值.
(2)结合(1)的结论,分t<2+2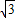 时,t=2+2
时,t=2+2 时,2+2
时,2+2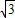 <t≤6时和6<t≤10+2
<t≤6时和6<t≤10+2 时四种情况分别求出△FMN面积的最值,最后综合讨论结果,可得答案.
时四种情况分别求出△FMN面积的最值,最后综合讨论结果,可得答案.
(3)利用勾股定理和两点之间的距离公式,分别讨论可得△FMN为直角三角形时的t值.
解答:解:以A为坐标原点,AB,AD为x,y轴正方向建立坐标系,
则A(0,0),B(6,0),C(6,4),D(0,4),F(2,4),M(0,4-t),N(6-t,0)
若MF=MN,则4+t2=(4-t)2+(6-t)2
即t2-20t+48=0
解得t=10±2
故t∈[0,10+2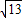 ]
]
(1)若F、M、N三点共线,则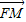 ∥
∥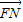
即(-2,-t)∥(4-t,-4)
即t2-4t-8=0
解得t=2+2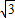
(2)①当t<2+2 时,如下图所示:
时,如下图所示:
S△FMN=SABCD-S△AMN-S△DMF-SNBFC
=4×6- ×(4-t)(6-t)-
×(4-t)(6-t)- ×2×t-
×2×t- ×(4+t)×4
×(4+t)×4
=- t2+2t+4,
t2+2t+4,
此时t=2时,S△FMN取最大值6
②当t=2+2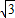 时,如下图所示:
时,如下图所示:
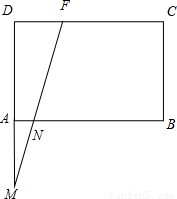
F、M、N三点共线,S△FMN=0
③当2+2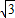 <t≤6时,如下图所示:
<t≤6时,如下图所示:

S△FMN= ×NE×DM=
×NE×DM= ×[
×[ -(6-t)]×t=
-(6-t)]×t= t2-2t-4,
t2-2t-4,
此时t=6时,S△FMN取最大值2
④当6<t≤10+2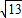 时,如下图所示:
时,如下图所示:

S△FMN= ×NE×DM=
×NE×DM= ×[(t-6)+
×[(t-6)+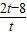 ]×t=
]×t= t2-2t-4,
t2-2t-4,
此时t=10+2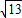 时,S△FMN取最大值52+16
时,S△FMN取最大值52+16
综上所述t=10+2 时,S△FMN取最大值52+16
时,S△FMN取最大值52+16
(3)若△FMN为直角三角形,
①若FM为斜边,则FM2=FN2+MN2,
即4+t2=(4-t)2+(6-t)2+(4-t)2+16
即t2-14t+40=0
解得t=4,或t=10
②若FN为斜边,则FN2=FM2+MN2,
即(4-t)2+(6-t)2=4+t2+(4-t)2+16
即12t=16
解得t=
③若MN为斜边,则MN2=FN2+FM2,
即4+t2+(4-t)2+(6-t)2=(4-t)2+16
即t2-8t+12=0
解得t=2,或t=6
综上所述△FMN为直角三角形,t=4,或t=10,或t= ,或t=2,或t=6
,或t=2,或t=6
点评:本题考查的知识点是函数单调性的应用,函数的最值,勾股定理,两点间距离公式,是函数图象与性质的综合应用,计算量较大.
(1)若F、M、N三点共线,则
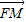 ∥
∥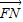 ,结合向量共线的充要条件,可求出满足条件的t值.
,结合向量共线的充要条件,可求出满足条件的t值.(2)结合(1)的结论,分t<2+2
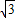 时,t=2+2
时,t=2+2 时,2+2
时,2+2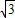 <t≤6时和6<t≤10+2
<t≤6时和6<t≤10+2 时四种情况分别求出△FMN面积的最值,最后综合讨论结果,可得答案.
时四种情况分别求出△FMN面积的最值,最后综合讨论结果,可得答案.(3)利用勾股定理和两点之间的距离公式,分别讨论可得△FMN为直角三角形时的t值.
解答:解:以A为坐标原点,AB,AD为x,y轴正方向建立坐标系,
则A(0,0),B(6,0),C(6,4),D(0,4),F(2,4),M(0,4-t),N(6-t,0)
若MF=MN,则4+t2=(4-t)2+(6-t)2
即t2-20t+48=0
解得t=10±2

故t∈[0,10+2
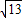 ]
](1)若F、M、N三点共线,则
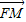 ∥
∥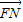
即(-2,-t)∥(4-t,-4)
即t2-4t-8=0
解得t=2+2
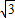
(2)①当t<2+2
 时,如下图所示:
时,如下图所示:
S△FMN=SABCD-S△AMN-S△DMF-SNBFC
=4×6-
 ×(4-t)(6-t)-
×(4-t)(6-t)- ×2×t-
×2×t- ×(4+t)×4
×(4+t)×4=-
 t2+2t+4,
t2+2t+4,此时t=2时,S△FMN取最大值6
②当t=2+2
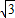 时,如下图所示:
时,如下图所示:
F、M、N三点共线,S△FMN=0
③当2+2
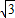 <t≤6时,如下图所示:
<t≤6时,如下图所示:
S△FMN=
 ×NE×DM=
×NE×DM= ×[
×[ -(6-t)]×t=
-(6-t)]×t= t2-2t-4,
t2-2t-4,此时t=6时,S△FMN取最大值2
④当6<t≤10+2
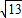 时,如下图所示:
时,如下图所示:
S△FMN=
 ×NE×DM=
×NE×DM= ×[(t-6)+
×[(t-6)+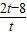 ]×t=
]×t= t2-2t-4,
t2-2t-4,此时t=10+2
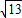 时,S△FMN取最大值52+16
时,S△FMN取最大值52+16
综上所述t=10+2
 时,S△FMN取最大值52+16
时,S△FMN取最大值52+16
(3)若△FMN为直角三角形,
①若FM为斜边,则FM2=FN2+MN2,
即4+t2=(4-t)2+(6-t)2+(4-t)2+16
即t2-14t+40=0
解得t=4,或t=10
②若FN为斜边,则FN2=FM2+MN2,
即(4-t)2+(6-t)2=4+t2+(4-t)2+16
即12t=16
解得t=

③若MN为斜边,则MN2=FN2+FM2,
即4+t2+(4-t)2+(6-t)2=(4-t)2+16
即t2-8t+12=0
解得t=2,或t=6
综上所述△FMN为直角三角形,t=4,或t=10,或t=
 ,或t=2,或t=6
,或t=2,或t=6点评:本题考查的知识点是函数单调性的应用,函数的最值,勾股定理,两点间距离公式,是函数图象与性质的综合应用,计算量较大.

练习册系列答案
相关题目
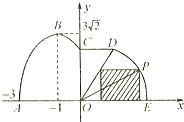 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为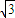 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时