题目内容
已知抛物线的顶点在坐标原点O,焦点F在x正半轴上,倾斜角为锐角的直线l过F点.设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,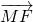 =λ
=λ ,其中λ>0
,其中λ>0
(I)若λ=1,求直线l的斜率;
(II)若点A、B在x轴上的射影分别为A1、B1,且|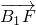 |,|
|,| |,2|
|,2|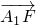 |成等差数列,求λ的值.
|成等差数列,求λ的值.
解:依题意设抛物线方程为y2=2px(p>0),A(x1,y1),B(x2,y2),直线l的斜率为k,k>0,M的纵坐标为y0,
则F( ,0),准线方程为x=-
,0),准线方程为x=- ,直线l的方程为y=k(x-
,直线l的方程为y=k(x- ),M(-
),M(- ,y0),y2>0
,y0),y2>0
因为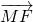 =λ
=λ ,所以(p,-y0)=λ(x2-
,所以(p,-y0)=λ(x2- ,y0),故p=λ(x2-
,y0),故p=λ(x2- )
)
(I)若λ=1,由p=λ(x2- ),y22=2px2,y2>0,得x2=
),y22=2px2,y2>0,得x2=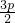 ,y2=
,y2= p,
p,
故点B的坐标为(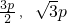 )
)
所以直线l的斜率k=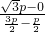 =
= (5分)
(5分)
(II)联立y2=2px,y=k(x- ),消去y,可得k2x2-(k2p+2p)x+
),消去y,可得k2x2-(k2p+2p)x+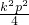 =0,则x1x2=
=0,则x1x2=
又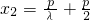 (7分)
(7分)
故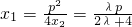 (9分)
(9分)
因为|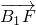 |,|
|,| |,2|
|,2|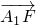 |成等差数列,
|成等差数列,
所以|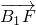 |+2|
|+2|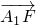 |=2|
|=2| |,
|,
故(x2- )+2(
)+2( -x1)=p,即x2-2x1=
-x1)=p,即x2-2x1=
将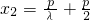 ,
,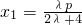 代入上式得
代入上式得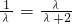
因为λ>0,所以λ=2. (12分)
分析:(I)先确定p=λ(x2- ),进而求出B的坐标,即可求直线l的斜率;
),进而求出B的坐标,即可求直线l的斜率;
(II)直线方程代入抛物线方程,求得A1、B1的横坐标,根据|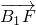 |,|
|,| |,2|
|,2|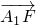 |成等差数列,可得|
|成等差数列,可得|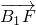 |+2|
|+2|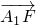 |=2|
|=2| |,从而可得x2-2x1=
|,从而可得x2-2x1= ,由此可求λ的值.
,由此可求λ的值.
点评:本题考查直线与抛物线的位置关系,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.
则F(
 ,0),准线方程为x=-
,0),准线方程为x=- ,直线l的方程为y=k(x-
,直线l的方程为y=k(x- ),M(-
),M(- ,y0),y2>0
,y0),y2>0因为
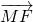 =λ
=λ ,所以(p,-y0)=λ(x2-
,所以(p,-y0)=λ(x2- ,y0),故p=λ(x2-
,y0),故p=λ(x2- )
)(I)若λ=1,由p=λ(x2-
 ),y22=2px2,y2>0,得x2=
),y22=2px2,y2>0,得x2=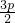 ,y2=
,y2= p,
p,故点B的坐标为(
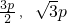 )
)所以直线l的斜率k=
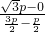 =
= (5分)
(5分)(II)联立y2=2px,y=k(x-
 ),消去y,可得k2x2-(k2p+2p)x+
),消去y,可得k2x2-(k2p+2p)x+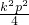 =0,则x1x2=
=0,则x1x2=
又
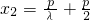 (7分)
(7分)故
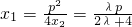 (9分)
(9分)因为|
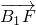 |,|
|,| |,2|
|,2|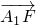 |成等差数列,
|成等差数列,所以|
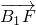 |+2|
|+2|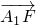 |=2|
|=2| |,
|,故(x2-
 )+2(
)+2( -x1)=p,即x2-2x1=
-x1)=p,即x2-2x1=
将
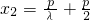 ,
,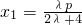 代入上式得
代入上式得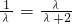
因为λ>0,所以λ=2. (12分)
分析:(I)先确定p=λ(x2-
 ),进而求出B的坐标,即可求直线l的斜率;
),进而求出B的坐标,即可求直线l的斜率;(II)直线方程代入抛物线方程,求得A1、B1的横坐标,根据|
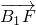 |,|
|,| |,2|
|,2|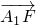 |成等差数列,可得|
|成等差数列,可得|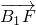 |+2|
|+2|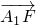 |=2|
|=2| |,从而可得x2-2x1=
|,从而可得x2-2x1= ,由此可求λ的值.
,由此可求λ的值.点评:本题考查直线与抛物线的位置关系,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐