Question

下表中的由平面到空间的三个类比推理正确的个数

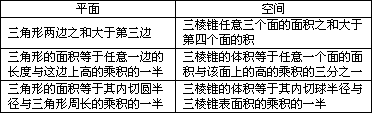
平面	空间
三角形两边之和大于第三边	三棱锥任意三个面的面积之和大于第四个面的面积
三角形的面积等于任意一边的长度与这边上高的乘积的一半	三棱锥的体积等于任意一个面的面积与该面上的高的乘积的三分之一
三角形的面积等于其内切圆半径与三角形周长的乘积的一半	三棱锥的体积等于其内切球半径与三棱锥表面积的乘积的一半

1. A.
   0
2. B.
   1
3. C.
   2
4. D.
   3

Answer 1

C
分析：本题是一个类比推理的问题．由两个平面中的结论与空间中的结论类比得出规律，对于表中的第一个命题，四面体的任意三个面的面积之和大于第四面的面积是正确的；根据锥体的体积公式知，第二个：三棱锥的体积等于任意一个面的面积与该面上的高的乘积的三分之一，也是正确的；再由此规律得出三角形的面积等于其内切圆半径与三角形周长乘积的的类比的空间中的结论：三棱锥的体积等于其内切球半径与三棱锥表面积的乘积的一半也是正确的．
解答：由题意，根据在平面内“三角形的两边之和大于第三边”类比在空间中
“四面体的任意三个面的面积之和大于第四面的面积，表中第一个命题正确．
对于第二个命题：
平面中的结论“三角形的面积等于任意一边的长度与这边上高的乘积的”类比空间中“三棱锥的体积等于任一底面的面积与这底面上的高的乘积的”
其规律是升维，面容类比体积，边长类比面积，周长类比全面积，是正确的结论；
平面中的结论“三角形的面积等于其内切圆半径与三角形周长乘积的”类比空间中的结论“三棱锥的体积等于其内切球半径与三棱锥全面积的乘积的”，故表中第三个结论是不正确的．
故选C．
点评：本题考查类比推理，本题解题的关键是正确理解类比的含义，注意本题所包含的三个命题都要判断正确，才能做对本题．