题目内容
(08年湖南卷理)(本小题满分13分)
若A、B是抛物线![]() 上的不同两点,弦AB(不平行于y轴)的垂直平分线与
上的不同两点,弦AB(不平行于y轴)的垂直平分线与
x轴相交于点P,则称弦AB是点P的一条“相关弦”.已知当![]() 时,点
时,点![]()
存在无穷多条“相关弦”.给定![]() .
.
(I)证明:点![]() 的所有“相关弦”的中点的横坐标相同;
的所有“相关弦”的中点的横坐标相同;
(II) 试问:点![]() 的“相关弦”的弦长中是否存在最大值?
的“相关弦”的弦长中是否存在最大值?
若存在,求其最大值(用x0表示):若不存在,请说明理由.
解: (I)设AB为点![]() 的任意一条“相关弦”,且点A、B的坐标分别是
的任意一条“相关弦”,且点A、B的坐标分别是
![]() ,则
,则![]() ,
,
两式相减得![]() .因为x1
.因为x1![]() x2,所以y1+y2
x2,所以y1+y2![]() 0.
0.
设直线AB的斜率是k,弦AB的中点是![]() ,则
,则
k=![]() .从而AB的垂直平分线l的方程为
.从而AB的垂直平分线l的方程为 ![]()
又点P(x0,0)在直线![]() 上,所以
上,所以 ![]()
而![]() 于是
于是![]() 故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.
故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.
(Ⅱ)由(Ⅰ)知,弦AB所在直线的方程是![]() ,代入
,代入![]() 中,
中,
整理得![]() (?)
(?)
则![]() 是方程(?)的两个实根,且
是方程(?)的两个实根,且![]()
设点P的“相关弦”AB的弦长为l,则
![]()
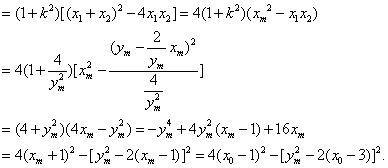
因为![]() ,于是设t=
,于是设t=![]() ,则t
,则t![]() (0,4x0-8).
(0,4x0-8).
记![]()
![]() .
.
若![]() ,则
,则![]() ,所以当
,所以当![]() ,即
,即![]() =2(x0-3)时,
=2(x0-3)时,
l有最大值![]() .
.
若![]() ,则
,则![]() ,
,![]() 在区间
在区间![]() 上是减函数,
上是减函数,
所以![]() ,l不存在最大值.
,l不存在最大值.
综上所述,当x0>3时,点![]() 的“相关弦”的弦长中存在最大值,且最大值
的“相关弦”的弦长中存在最大值,且最大值
为2(x0-1);当2< x0![]() 3时,点
3时,点![]() 的“相关弦”的弦长中不存在最大值.
的“相关弦”的弦长中不存在最大值.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
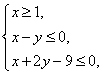 则
则