题目内容
已知两定点F1(-
,0),F2(
,0),点P是曲线E上任意一点,且满足条件|
|-|
|=2.
①求曲线E的轨迹方程;
②若直线y=kx-1与曲线E交于不同两点A,B两点,求k的范围.
| 2 |
| 2 |
| PF2 |
| PF1 |
①求曲线E的轨迹方程;
②若直线y=kx-1与曲线E交于不同两点A,B两点,求k的范围.
分析:①由双曲线的定义可知,曲线E是以F1(-
,0),F2(
,0)为焦点的双曲线的左支,由此可求曲线E的方程;
②由题意建立方程组
消去y,得(1-k2)x2+2kx-2=0,根据直线与双曲线左支交于两点A,B,建立不等式组,即可求得k的范围.
| 2 |
| 2 |
②由题意建立方程组
|
解答: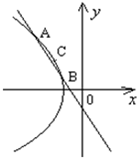 解:①由双曲线的定义可知,曲线E是以F1(-
解:①由双曲线的定义可知,曲线E是以F1(-
,0),F2(
,0)为焦点的双曲线的左支,且c=
,a=1,
∴b=
=1
故曲线E的方程为:x2-y2=1(x<0)
②设A(x1,y1),B(x2,y2),由题意建立方程组
消去y,得(1-k2)x2+2kx-2=0
已知直线与双曲线左支交于两点A,B,有
解得:-
<k<-1
 解:①由双曲线的定义可知,曲线E是以F1(-
解:①由双曲线的定义可知,曲线E是以F1(-| 2 |
| 2 |
| 2 |
∴b=
| c2-a2 |
故曲线E的方程为:x2-y2=1(x<0)
②设A(x1,y1),B(x2,y2),由题意建立方程组
|
已知直线与双曲线左支交于两点A,B,有
|
| 2 |
点评:本题考查轨迹方程,考查直线与双曲线的位置关系,解题的关键是正确运用双曲线的定义与韦达定理.

练习册系列答案
相关题目