题目内容
已知y=f（x）与y=g（x）都为R上的可导函数，且f′（x）＞g′（x），则下面不等式正确的是（ ）
| A．f（2）+g（1）＞f（1）+g（2） |
| B．f（1）+f（2）＞g（1）+g（2） |
| C．f（1）﹣f（2）＞g（1）﹣g（2） |
| D．f（2）﹣g（1）＞f（1）﹣g（2） |
A
解析
练习册系列答案
相关题目
函数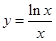
的最大值为（ ）
A． | B． | C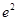． | D． |
函数
=
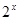的导函数是（ ）
A．y′=3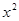 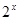| B．y′=2 |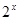
C．y′=3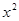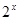+ 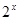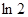| D．y′=3+ |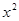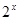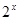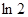
若函数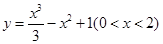
的图象上任意点处切线的倾斜角为
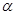，则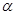的最小值是（ ）
A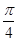． | B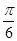． | C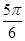． | D． |
下列求导运算正确的是（ ）
A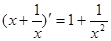． | B． |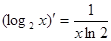
C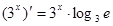． | D． |
设函数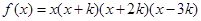
，且
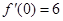，则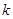
（ ）
| A．0 | B．－1 | C．3 | D．－6 |
若曲线y=x2+ax+b在点（0，b）处的切线方程是x﹣y+1=0，则（ ）
| A．a=1，b=1 | B．a=﹣1，b=1 |
| C．a=1，b=﹣1 | D．a=﹣1，b=﹣1 |
若规定
，不等式
对一切x∈（0，1]恒成立，则实数m的最大值为（ ）
| A．0 | B．2 | C． | D．3 |
f（x）=x3﹣3x2+2在区间[﹣1，1]上的最大值是（ ）
| A．﹣2 | B．0 | C．2 | D．4 |