题目内容
【题目】选修4-5:不等式选讲
已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)解关于![]() 的不等式
的不等式![]() .
.
【答案】解:(Ⅰ)当a=3时,f(x)=|x-3|-2|x-1|=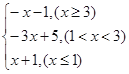 ……3分
……3分
所以,当x=1时,函数f(x)取得最大值2. ……5分
(Ⅱ)由f(x)>0得|x-a|≥4|x-1|,
两边平方得:(x-a)2≥4(x-1),
即3x2+2(a-4)x+4-a2≤0, ……7分
得(x-(2-a))(3x-(2+a))≤0,
所以,①当a>1时,不等式的解集为(2-a,![]() );
);
②当a=1时,不等式的解集为{x|x=1};
③当a<1时,不等式的解集为(![]() , 2-a). ……10分
, 2-a). ……10分
【解析】
试题(1)当![]() 是,函数可去掉绝对值化为分段函数,再根据函数的单调性求得函数
是,函数可去掉绝对值化为分段函数,再根据函数的单调性求得函数![]() 的最大值;(2)关于
的最大值;(2)关于![]() 的不等式即
的不等式即![]() ,化简可得
,化简可得![]() ,由此可求得一元二次不等式的解集.
,由此可求得一元二次不等式的解集.
试题解析:(1)当![]() 时,
时,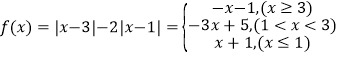
所以当![]() ,函数
,函数![]() 取得最大值2.
取得最大值2.
(2)由![]() ,得
,得![]()
两边平方,得![]()
即![]()
得![]() ,
,
所以当![]() 时,不等式的解集为
时,不等式的解集为![]()
当![]() 时,不等式的解集为
时,不等式的解集为![]()
当![]() ,不等式的解集为
,不等式的解集为![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目