题目内容
已知:长方体 ,
,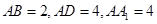 ,
, 为对角线
为对角线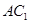 的中点,过
的中点,过 的直线与长方体表面交于两点
的直线与长方体表面交于两点 ,
, 为长方体表面上的动点,则
为长方体表面上的动点,则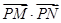 的取值范围是 .
的取值范围是 .
 .
.
解析试题分析:如图所示.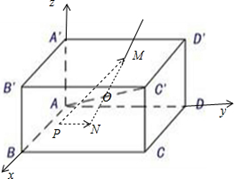
∵O为对角线AC1的中点,∴O(1,2,2).以下分类讨论:根据长方体的对称性和数量积的性质:取P点时只要取顶点和每个表面的中心即可.
①当点MN在上下两个面时.取P(0,0,0),设N(x,y,0),(0≤x≤2,0≤y≤4).则M(2-x,4-y,4).∴ =x(2-x)+y(4-y)=-[(x-1)2+(y-2)2]+5,此时可得:
=x(2-x)+y(4-y)=-[(x-1)2+(y-2)2]+5,此时可得: 的取值范围是[0,5].
的取值范围是[0,5].
取点P(1,0,2), =(1-x,4-y,-2),
=(1-x,4-y,-2),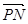 =(x-1,y,-2)
=(x-1,y,-2)
则 =-(x-1)2+y(4-y)-4=-[(x-1)2+(y-2)2],
=-(x-1)2+y(4-y)-4=-[(x-1)2+(y-2)2],
由于0≤x≤2,0≤y≤4,∴-5≤ ≤0.
≤0.
此时可得: 的取值范围是[-5,0].
的取值范围是[-5,0].
综上可得: 的取值范围是[-5,5].
的取值范围是[-5,5].
②当点MN在左右两个面时, 的取值范围是[-5,5].
的取值范围是[-5,5].
③当点MN分别上或下两个面、左或右时, 的取值范围是[-8,8].
的取值范围是[-8,8].
综上可得: 的取值范围是[-8,8].
的取值范围是[-8,8].
故应填入: [-8,8].
考点:1.长方体的对称性;2.数量积的性质.

练习册系列答案
相关题目
如图,在△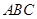 中,
中,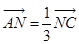 ,
,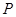 是
是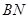 上的一点,若
上的一点,若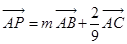 ,则实数
,则实数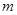 的值为( )
的值为( )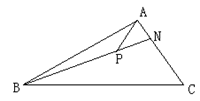
A.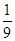 | B.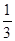 | C.1 | D.3 |
若|a|="5," |b|="6," <a,b>= ,则a.b=( )
,则a.b=( )
| A. 15 | B. 15 | C. 15 | D. 10 |
设向量a,b均为单位向量,且|a+b|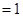 ,则a与b夹角为 ( )
,则a与b夹角为 ( )
A.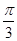 | B.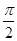 | C. | D.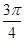 |
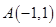 、
、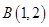 、
、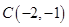 、
、 ,则向量
,则向量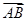 在
在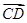 方向上的投影为 .
方向上的投影为 .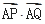 的取值范围是________.
的取值范围是________.
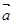 与
与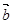 的夹角为
的夹角为 ,且
,且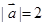 ,
,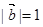 ,则
,则 .
.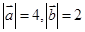 ,且
,且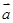 与
与 夹角为
夹角为 ,则
,则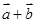 的夹角是 .
的夹角是 .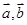 满足
满足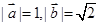 ,
,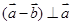 , 向量
, 向量 与
与 的夹角为________.
的夹角为________.