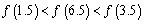题目内容
设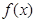 是定义在
是定义在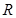 上以
上以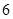 为周期的函数,
为周期的函数,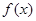 在
在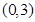 内单调递减,且
内单调递减,且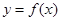 的图象关于直线
的图象关于直线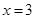 对称,则下面正确的结论是( )
对称,则下面正确的结论是( )
A.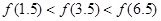 | B.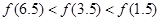 |
C.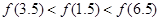 | D.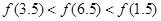 |
B
解析考点:奇偶函数图象的对称性;函数单调性的性质;函数的周期性.
专题:计算题.
分析:由函数f(x)的周期为6,从而有f(x+6)=f(x),所以有f(6.5)=f(0.5),f(3.5)=f(2.5),又因为0<0.5<1.5<2.5<3,且函数在(0,3)内单调递减,从而判断大小
解答:解:f(x)在R上以6为周期,对称轴为x=3,且在(0,3)内单调递减,f(3.5)=f(2.5),f(6.5)=f(0.5)
∵0.5<1.5<2.5
∴f(2.5)<f(1.5)<f(0.5)
即f(3.5)<f(1.5)<f(6.5)
故选 B
点评:本题主要考查了函数的周期性与单调性的综合运用,利用周期性把所要比较的变量转化到同一单调区间,利用函数的单调性比较函数值的大小,是解决此类问题的常用方法.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
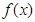 是定义在
是定义在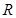 上以
上以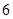 为周期的函数,
为周期的函数,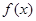 在
在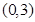 内单调递减,且
内单调递减,且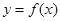 的图象关于直线
的图象关于直线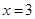 对称,则下面正确的结论是(
)
对称,则下面正确的结论是(
)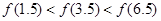 B.
B.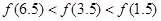
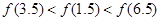 D.
D.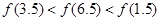
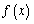 是定义在
是定义在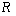 上以
上以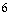 为周期的函数,函数
为周期的函数,函数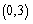 上单调递减,且
上单调递减,且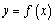 的图像关于直线
的图像关于直线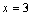 对称,则下面结论中正确的是 (
)
对称,则下面结论中正确的是 (
)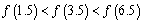 B.
B. 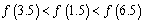
 D.
D. 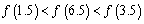
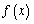 是定义在
是定义在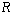 上以
上以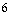 为周期的函数,函数
为周期的函数,函数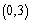 上单调递减,且
上单调递减,且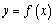 的图像关于直线
的图像关于直线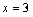 对称,则下面结论中正确的是 (
)
对称,则下面结论中正确的是 (
)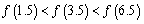 B.
B. 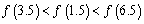
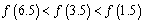 D.
D.