题目内容
已知a≠0,函数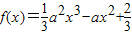 ,g(x)=-ax+1,x∈R.
,g(x)=-ax+1,x∈R.(I)求函数f(x)的单调递减区间;
(Ⅱ)若在区间
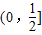 上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.
上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.
【答案】分析:(1)对函数f(x)进行求导,当f'(x)<0时的x的区间即是原函数的单调递减区间.
(2)令F(x)=f(x)-g(x),只要函数F(x)在区间(0, ]上的最大值大于0即可得到答案.
]上的最大值大于0即可得到答案.
解答:解:(I)由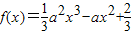 求导得,f'(x)=a2x2-2ax.
求导得,f'(x)=a2x2-2ax.
①当a>0时,由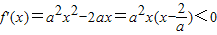 ,解得
,解得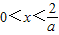
所以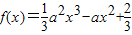 在
在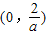 上递减.
上递减.
②当a<0时,由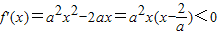 可得
可得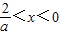
所以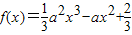 在
在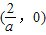 上递减.
上递减.
综上:当a>0时,f(x)单调递减区间为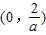 ;
;
当a<0时,f(x)单调递减区间为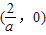
(Ⅱ)设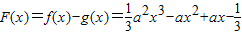
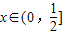 .
.
对F(x)求导,得F'(x)=a2x2-2ax+a=a2x2+a(1-2x),
因为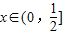 ,a>0,所以F'(x)=a2x2+a(1-2x)>0,F(x)在区间
,a>0,所以F'(x)=a2x2+a(1-2x)>0,F(x)在区间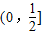 上为增函数,则
上为增函数,则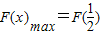 .
.
依题意,只需F(x)max>0,即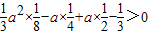 ,
,
即a2+6a-8>0,解得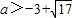 或
或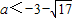 (舍去).
(舍去).
所以正实数a的取值范围是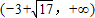 .
.
点评:本题主要考查通过求导求函数增减性的问题.当导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
(2)令F(x)=f(x)-g(x),只要函数F(x)在区间(0,
 ]上的最大值大于0即可得到答案.
]上的最大值大于0即可得到答案.解答:解:(I)由
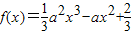 求导得,f'(x)=a2x2-2ax.
求导得,f'(x)=a2x2-2ax.①当a>0时,由
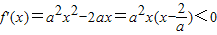 ,解得
,解得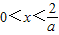
所以
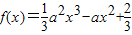 在
在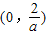 上递减.
上递减.②当a<0时,由
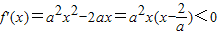 可得
可得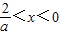
所以
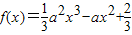 在
在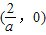 上递减.
上递减.综上:当a>0时,f(x)单调递减区间为
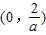 ;
;当a<0时,f(x)单调递减区间为
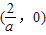
(Ⅱ)设
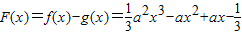
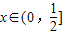 .
.对F(x)求导,得F'(x)=a2x2-2ax+a=a2x2+a(1-2x),
因为
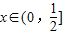 ,a>0,所以F'(x)=a2x2+a(1-2x)>0,F(x)在区间
,a>0,所以F'(x)=a2x2+a(1-2x)>0,F(x)在区间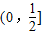 上为增函数,则
上为增函数,则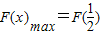 .
.依题意,只需F(x)max>0,即
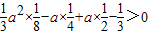 ,
,即a2+6a-8>0,解得
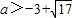 或
或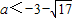 (舍去).
(舍去).所以正实数a的取值范围是
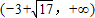 .
.点评:本题主要考查通过求导求函数增减性的问题.当导数大于0时原函数单调递增,当导数小于0时原函数单调递减.

练习册系列答案
相关题目
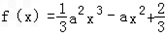 ,g(x)=﹣ax+1,x∈R.
,g(x)=﹣ax+1,x∈R.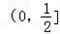 上至少存在一个实数x0,使f(x0)>g(x0)成立,
上至少存在一个实数x0,使f(x0)>g(x0)成立,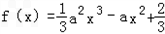 ,g(x)=﹣ax+1,x∈R.
,g(x)=﹣ax+1,x∈R.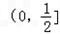 上至少存在一个实数x0,使f(x0)>g(x0)成立,试求正实数a的取值范围。
上至少存在一个实数x0,使f(x0)>g(x0)成立,试求正实数a的取值范围。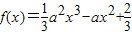 ,g(x)=-ax+1,x∈R.
,g(x)=-ax+1,x∈R.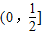 上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.
上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.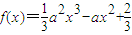 ,g(x)=-ax+1,x∈R.
,g(x)=-ax+1,x∈R.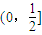 上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.
上至少存在一个实数x,使f(x)>g(x)成立,试求正实数a的取值范围.