题目内容
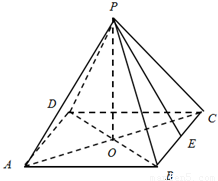
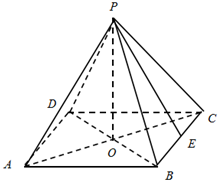 如图,设计一个小型正四棱锥形冷水塔,其中顶点P在底面的射影为正方形ABCD的中心O,返水口E为BC的中点,冷水塔的四条钢梁(侧棱)设计长度均为10米.冷水塔的侧面选用钢板,基于安全与冷凝速度的考量,要求钢梁(侧棱)与底面的夹角α落在区间[
如图,设计一个小型正四棱锥形冷水塔,其中顶点P在底面的射影为正方形ABCD的中心O,返水口E为BC的中点,冷水塔的四条钢梁(侧棱)设计长度均为10米.冷水塔的侧面选用钢板,基于安全与冷凝速度的考量,要求钢梁(侧棱)与底面的夹角α落在区间[| π |
| 6 |
| π |
| 3 |
分析:根据题意,算出底面边长等于10
cosα,从而在Rt△P0E中算出PE=5
•
,可得侧面积关于α的函数关系式:S侧面=200
,由sinα∈[
,
]即可算出当α=
时,侧面钢板用料最省.由此可得相应的底面边长和高,得到本题答案.
| 2 |
| 2 |
| 1+sin2α |
| 1-sin4α |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
解答:解:依题意,可得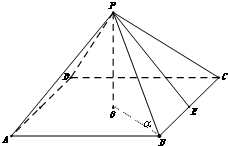
钢梁(侧棱)与底面的夹角为∠PBO=α.
∴OP=10sinα,-------------------------(2分)
则OE=
OB=5
cosα,
可得BC=10
cosα---------(4分)
在Rt△POE中,
PE=
=5
•
,---(6分)
∴S侧面=4×(
PE•BC)=200cosα
-------(8分)
=200
----------------------------(10分)
又∵α∈[
,
],可得
≤sinα≤
,----------(11分)
∴当且仅当sinα=
时,侧面积取得最小值,等于200
=50
---------------(13分)
此时的cosα=
,AB=5
,OP=5
.
即冷水塔的底面边长应设计为AB=5
米,高OP=5
米时,侧面钢板用料最省--------(14分)

钢梁(侧棱)与底面的夹角为∠PBO=α.
∴OP=10sinα,-------------------------(2分)
则OE=
| ||
| 2 |
| 2 |
可得BC=10
| 2 |
在Rt△POE中,
PE=
| OP2+OE2 |
| 2 |
| 1+sin2α |
∴S侧面=4×(
| 1 |
| 2 |
| 1+sin2α |
=200
| 1-sin4α |
又∵α∈[
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴当且仅当sinα=
| ||
| 2 |
1-(
|
| 7 |
此时的cosα=
| 1 |
| 2 |
| 2 |
| 3 |
即冷水塔的底面边长应设计为AB=5
| 2 |
| 3 |
点评:本题给出实际应用问题,求侧面积的最小值.着重考查了正棱锥的性质、直线与平面所成角、解直角三角形和三角函数模型的应用等知识,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
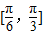 内,如何设计可得侧面钢板用料最省且符合施工要求?
内,如何设计可得侧面钢板用料最省且符合施工要求?