题目内容
设函数 ,若关于
,若关于 的方程
的方程 在
在 上恰好有两个相异实根,则实数
上恰好有两个相异实根,则实数 的取值范围为______________.
的取值范围为______________.
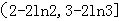
解析试题分析:方程f(x)=x2+x+a可化为x-a+1-ln(1+x)2=0,由于此方程为非基本方程,故求方程的根,可以转化为求对应函数的零点问题,利用导数法我们易构造出满足条件的不等式组,解不等式组即可得到实数a的取值范围.解:若f(x)=x2+x+a,即(1+x)2-ln(1+x)2=x2+x+a,即x-a+1-ln(1+x)2=0,记g(x)=x-a+1-ln(1+x)2,则g'(x)=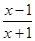 ,令g'(x)>0,得x>1,或x<-1,令g'(x)<0,得-1<x<1,∴g(x)在[0,1]上单调递减,在[1,2]上单调递增;,若方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,则,g(0)≥0,g(1)<0,g(2)≥0,解得2-2ln2<a≤3-2ln3,故答案为:(2-2ln2,3-2ln3]
,令g'(x)>0,得x>1,或x<-1,令g'(x)<0,得-1<x<1,∴g(x)在[0,1]上单调递减,在[1,2]上单调递增;,若方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,则,g(0)≥0,g(1)<0,g(2)≥0,解得2-2ln2<a≤3-2ln3,故答案为:(2-2ln2,3-2ln3]
考点:方程的根的分布
点评:本题考查的知识点是方程的根的分布,其中利用方程的根与对应函数之间的关系,将方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,转化为对应函数在区间∈[0,2]上恰好有两个相异的零点是解答本题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
已知幂函数 的部分对应值如图表:则不等式
的部分对应值如图表:则不等式 的解集是
的解集是
| x | 1 |  |
| f(x) | 1 |  |
 是幂函数,且在
是幂函数,且在 上是增函数,则实数
上是增函数,则实数 .
.  的平方根是 .
的平方根是 . (
( )的图象恒过定点A,若点A也在函数
)的图象恒过定点A,若点A也在函数 的图象上,则
的图象上,则 = .
= .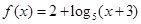 在区间[-2,2]上的值域是____________
在区间[-2,2]上的值域是____________ =_______。
=_______。 的图象过点
的图象过点 ,则
,则 = ;
= ; ,则
,则 的最大值为_ .
的最大值为_ .