题目内容
已知M={(x,y)|y=2x+1},N={(x,y)|y=-ax+2},M∩N≠Φ的充要条件 .
答案:a=-2
解析:
解析:
|
解:由 M∩N≠Φ可知2x+1=-ax+2有解,即(2+a)x=1有解可得a+2≠0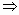 a=-2. a=-2. |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
已知M={(x,y)|y=2x+1},N={(x,y)|y=-ax+2},M∩N≠Φ的充要条件 .
|
解:由 M∩N≠Φ可知2x+1=-ax+2有解,即(2+a)x=1有解可得a+2≠0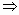 a=-2. a=-2. |

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案