题目内容
设
答案:
解析:
解析:
| 设等差数列{an}的公差为d,则an=a1+(n-1)d。
∴bn= 由 代入已知条件 解这个方程组得b1=2,b3= ∴a1=-1,d=2或a1=3,d=-2, 因此,当a1=-1,d=2时an=a1+(n-1)d=2n-3。 当a1=3,d=-2时,an=
|

练习册系列答案
相关题目
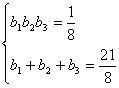
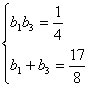
 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知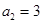 ,
,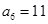 ,则
,则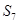 等于( )
等于( ) 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知 则
则 等于 (
)
等于 (
)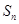 是等差数列
是等差数列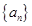 的前n项和,已知
的前n项和,已知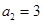 ,
,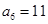 ,则
,则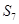 等于(
)
等于(
) 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知 ,
, ,则
,则 等于( )
等于( )  是等差数列
是等差数列 的前
的前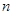 项和,已知
项和,已知 ,
,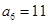 ,则
,则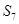 等于( )
等于( )