题目内容
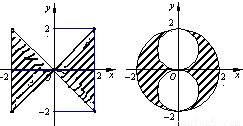
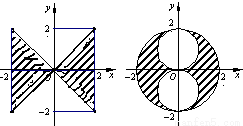
(理)由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1;满足x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2,试写出V1与V2的一个关系式V1:V2= .
【答案】分析:由于旋转体的体积为V1由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体,利用体积的分割法可知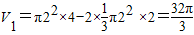 ,
,
而旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,利用体积分割法可以求得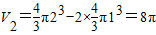 ,进而可得关系式V1:V2.
,进而可得关系式V1:V2.
解答:解:因为旋转体的体积为V1由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体,它旋转之后应该构成的是一个圆柱内减去两个体积全等的圆锥的体积,即:利用体积的分割法可知 ,又旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,它应该为一个大的球体减去两个球半径一样的小的球体,即:
,又旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,它应该为一个大的球体减去两个球半径一样的小的球体,即: ,所以可得关系式V1:V2=4:3.
,所以可得关系式V1:V2=4:3.
故答案为:4:3.
点评:此题考查了球体的体积公式,圆柱的体积公式及圆锥的体积公式,还考查了学生空间的想象能力及计算技能.
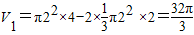 ,
,而旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,利用体积分割法可以求得
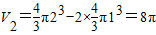 ,进而可得关系式V1:V2.
,进而可得关系式V1:V2.解答:解:因为旋转体的体积为V1由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体,它旋转之后应该构成的是一个圆柱内减去两个体积全等的圆锥的体积,即:利用体积的分割法可知
 ,又旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,它应该为一个大的球体减去两个球半径一样的小的球体,即:
,又旋转体的体积为V2x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体,它应该为一个大的球体减去两个球半径一样的小的球体,即: ,所以可得关系式V1:V2=4:3.
,所以可得关系式V1:V2=4:3.故答案为:4:3.
点评:此题考查了球体的体积公式,圆柱的体积公式及圆锥的体积公式,还考查了学生空间的想象能力及计算技能.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
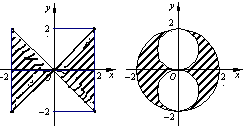 (理)由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1;满足x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2,试写出V1与V2的一个关系式V1:V2=
(理)由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1;满足x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2,试写出V1与V2的一个关系式V1:V2=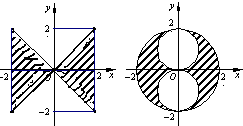 (理)由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1;满足x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2,试写出V1与V2的一个关系式V1:V2=________.
(理)由曲线y=|x|,y=-|x|,x=2,x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1;满足x2+y2≤4,x2+(y-1)2≥1,x2+(y+1)2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2,试写出V1与V2的一个关系式V1:V2=________.