题目内容
(本题16分)
已知公差不为0的等差数列{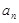 }的前4项的和为20,且
}的前4项的和为20,且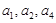 成等比数列;
成等比数列;
(1)求数列{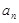 }通项公式;(2)设
}通项公式;(2)设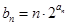 ,求数列{
,求数列{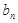 }的前n项的和
}的前n项的和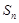 ;
;
(3)在第(2)问的基础上,是否存在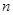
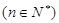 使得
使得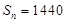 成立?若存在,求出所有解;若不存在,请说明理由.
成立?若存在,求出所有解;若不存在,请说明理由.
【答案】
(1) 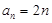 .(2)
.(2)
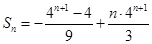 ;(3)无解.
;(3)无解.
【解析】
根据条件等差数列{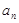 }的前4项的和为20,且
}的前4项的和为20,且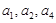 成等比数列,转化为关于
成等比数列,转化为关于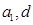 的方程
的方程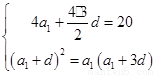 ,解得;
,解得;
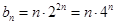 是差比数列,求和用错位相减法,注意次数的对齐;
是差比数列,求和用错位相减法,注意次数的对齐;
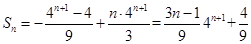 ,
, 随着n的增大而增大,试验n,解得
随着n的增大而增大,试验n,解得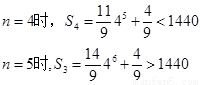 ,无解。
,无解。
解:(1)由题可知
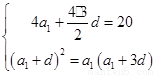 解得
解得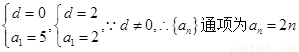 .
.
(2)当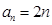 ,
,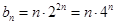 ,
,
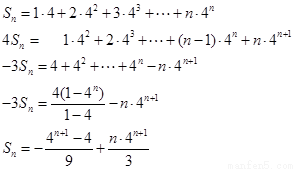
(3)当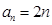 ,
,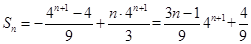 ,
,
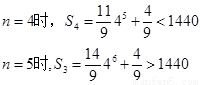
所以无解.

练习册系列答案
相关题目
 满足满足
满足满足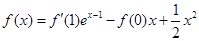 ;
;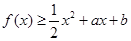 ,求
,求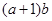 的最大值.
的最大值.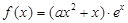 ,其中e是自然数的底数,
,其中e是自然数的底数,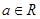 ,
,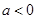 时,解不等式
时,解不等式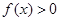 ;
;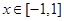 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;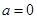 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程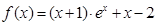 在
在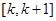
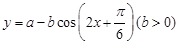 的最大值为
的最大值为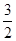 ,最小值为
,最小值为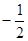 .
.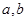 的值;
的值;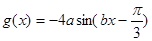 的最小值并求出对应x的集合.
的最小值并求出对应x的集合. 的最大值为
的最大值为 ,最小值为
,最小值为 .
. 的值;
的值; 的最小值并求出对应x的集合.
的最小值并求出对应x的集合.