题目内容
嘉兴市秀洲区为促进淡水鱼养殖业的发展,将价格控制在适当范围内,并决定对淡水鱼养殖提供政府补贴.设淡水鱼的市场价格为x元/kg,政府补贴为t元/kg.根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量Pkg与市场日需求量Qkg近似满足关系:P=1000(x+t-8)(x≥8,t≥0),Q=500
(8≤x≤14);当P=Q时的市场价格称为市场平衡价格.
(1)将政府补贴费表示为市场平衡价格的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于10元/kg,政府需要补贴吗?如果需要,至少为多少元/kg?
| 26-x |
(1)将政府补贴费表示为市场平衡价格的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于10元/kg,政府需要补贴吗?如果需要,至少为多少元/kg?
分析:(1)据当p=Q时市场价格达到市场平衡价格,列出关于x,t的等式即可求出函数关系式,
(2)由x≤10,换元可得二次函数,求出此时的t的取值范围,即为所求.
(2)由x≤10,换元可得二次函数,求出此时的t的取值范围,即为所求.
解答:解:(1)依题设有1000(x+t-8)=500
∴t=8-x+
(8≤x≤14);
(2)令m=
,∵8≤x≤10,∴4≤m≤3
∴t=m2+
-18=(m+
)2-
-18
∵4≤m≤3
∴0≤t≤
∴政府不需要补贴.
| 26-x |
∴t=8-x+
| 1 |
| 2 |
| 26-x |
(2)令m=
| 26-x |
| 2 |
∴t=m2+
| m |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
∵4≤m≤3
| 2 |
∴0≤t≤
3
| ||
| 2 |
∴政府不需要补贴.
点评:本小题主要考查运用所学数学知识和方法解决实际问题的能力,以及函数的概念、方程和不等式的解法等基础知识和方法.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 ,政府补贴为
,政府补贴为 。根据市场调查,当
。根据市场调查,当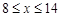 时,淡水鱼的市场日供应量
时,淡水鱼的市场日供应量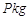 与市场日需求量
与市场日需求量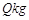 近似满足关系:
近似满足关系: ,
,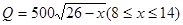 ;当
;当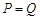 时的市场价格称为市场平衡价格。
时的市场价格称为市场平衡价格。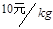 ,政府需要补贴吗?如果需要,至少为多少
,政府需要补贴吗?如果需要,至少为多少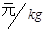 ?
? ;当P=Q时的市场价格称为市场平衡价格.
;当P=Q时的市场价格称为市场平衡价格.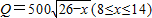 ;当P=Q时的市场价格称为市场平衡价格.
;当P=Q时的市场价格称为市场平衡价格.