题目内容
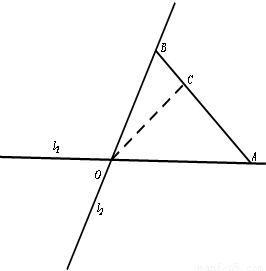
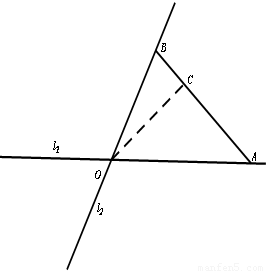
如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=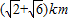 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.(1)求y关于x的函数关系式并指出它的定义域;
(2)试确定点A、B的位置,使△OAB的面积最小.
【答案】分析:(1)根据△AOC的面积与△BOC的面积之和等于△AOB的面积,可得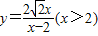 .
.
(2)根据△OAB的面积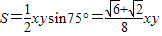 ,化简为
,化简为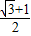 [(x-2)+
[(x-2)+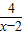 +4],再利用基本不等式求出
+4],再利用基本不等式求出
它的最小值.
解答:(1)因为△AOC的面积与△BOC的面积之和等于△AOB的面积,
所以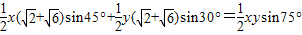 ,…(4分)
,…(4分)
即 ,所以,
,所以,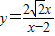 ,它的定义域为(2,+∞).…(6分)
,它的定义域为(2,+∞).…(6分)
(2)△OAB的面积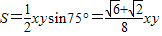 =
=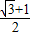 •
•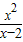 …(8分)
…(8分)
=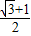 •
•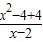 =
=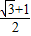 [(x+2)+
[(x+2)+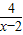 ]=
]=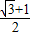 [(x-2)+
[(x-2)+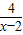 +4]
+4]
≥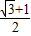 •(2
•(2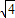 +4)=4(
+4)=4(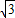 +1). …(12分)
+1). …(12分)
当且仅当x=4时取等号,此时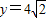 .
.
故当OA=4km, 时,△OAB面积的最小值为
时,△OAB面积的最小值为 . …(14分)
. …(14分)
点评:本题主要考查求函数的解析式和定义域,基本不等式的应用,属于基础题.
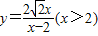 .
.(2)根据△OAB的面积
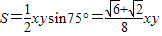 ,化简为
,化简为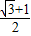 [(x-2)+
[(x-2)+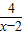 +4],再利用基本不等式求出
+4],再利用基本不等式求出它的最小值.
解答:(1)因为△AOC的面积与△BOC的面积之和等于△AOB的面积,
所以
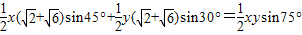 ,…(4分)
,…(4分)即
 ,所以,
,所以,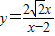 ,它的定义域为(2,+∞).…(6分)
,它的定义域为(2,+∞).…(6分)(2)△OAB的面积
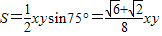 =
=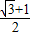 •
•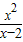 …(8分)
…(8分)=
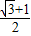 •
•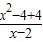 =
=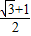 [(x+2)+
[(x+2)+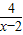 ]=
]=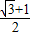 [(x-2)+
[(x-2)+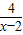 +4]
+4]≥
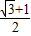 •(2
•(2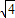 +4)=4(
+4)=4(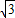 +1). …(12分)
+1). …(12分)当且仅当x=4时取等号,此时
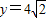 .
.故当OA=4km,
 时,△OAB面积的最小值为
时,△OAB面积的最小值为 . …(14分)
. …(14分)点评:本题主要考查求函数的解析式和定义域,基本不等式的应用,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 (2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=
(2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=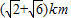 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
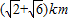 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.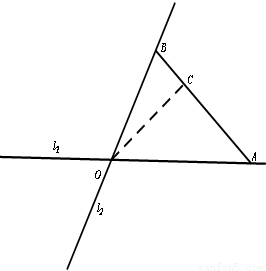
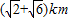 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.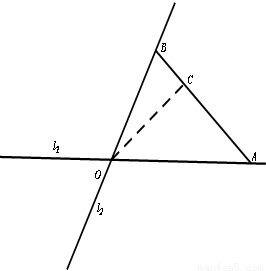
 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.