题目内容
若关于x的不等式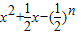 ≥0对任意n∈N*在x∈(-∞,λ]恒成立,则实常数λ的取值范围是 .
≥0对任意n∈N*在x∈(-∞,λ]恒成立,则实常数λ的取值范围是 .
【答案】分析:关于x的不等式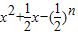 ≥0对任意n∈N*在x∈(-∞,λ]恒成立,等价于
≥0对任意n∈N*在x∈(-∞,λ]恒成立,等价于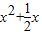 ≥
≥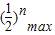 对任意n∈N*在x∈(-∞,λ]恒成立,由
对任意n∈N*在x∈(-∞,λ]恒成立,由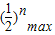 =
= ,知
,知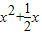
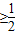 对 x∈(-∞,λ]恒成立.由此能求出λ的范围.
对 x∈(-∞,λ]恒成立.由此能求出λ的范围.
解答:解:关于x的不等式 ≥0对任意n∈N*在x∈(-∞,λ]恒成立,
≥0对任意n∈N*在x∈(-∞,λ]恒成立,
等价于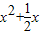 ≥
≥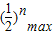 对任意n∈N*在x∈(-∞,λ]恒成立,
对任意n∈N*在x∈(-∞,λ]恒成立,
∵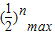 =
= ,
,
∴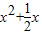
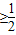 对 x∈(-∞,λ]恒成立.
对 x∈(-∞,λ]恒成立.
设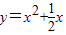 ,它的图象是开口向上,对称轴为x=-
,它的图象是开口向上,对称轴为x=- 的抛物线,
的抛物线,
∴当x≤- 时,左边是单调减的,所以要使不等式恒成立,则λ2+
时,左边是单调减的,所以要使不等式恒成立,则λ2+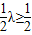 ,
,
解得λ≤-1,或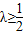 (舍)
(舍)
当x>- ,左边的最小值就是在x=-
,左边的最小值就是在x=- 时取到,
时取到,
达到最小值时,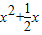 =
=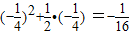 ,不满足不等式.
,不满足不等式.
因此λ的范围就是 λ≤-1.
故答案为:(-∞,-1].
点评:本题考查函数恒成立问题的应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
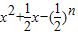 ≥0对任意n∈N*在x∈(-∞,λ]恒成立,等价于
≥0对任意n∈N*在x∈(-∞,λ]恒成立,等价于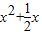 ≥
≥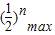 对任意n∈N*在x∈(-∞,λ]恒成立,由
对任意n∈N*在x∈(-∞,λ]恒成立,由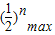 =
= ,知
,知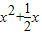
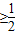 对 x∈(-∞,λ]恒成立.由此能求出λ的范围.
对 x∈(-∞,λ]恒成立.由此能求出λ的范围.解答:解:关于x的不等式
 ≥0对任意n∈N*在x∈(-∞,λ]恒成立,
≥0对任意n∈N*在x∈(-∞,λ]恒成立,等价于
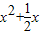 ≥
≥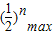 对任意n∈N*在x∈(-∞,λ]恒成立,
对任意n∈N*在x∈(-∞,λ]恒成立,∵
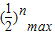 =
= ,
,∴
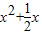
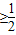 对 x∈(-∞,λ]恒成立.
对 x∈(-∞,λ]恒成立.设
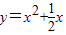 ,它的图象是开口向上,对称轴为x=-
,它的图象是开口向上,对称轴为x=- 的抛物线,
的抛物线,∴当x≤-
 时,左边是单调减的,所以要使不等式恒成立,则λ2+
时,左边是单调减的,所以要使不等式恒成立,则λ2+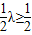 ,
,解得λ≤-1,或
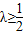 (舍)
(舍)当x>-
 ,左边的最小值就是在x=-
,左边的最小值就是在x=- 时取到,
时取到,达到最小值时,
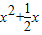 =
=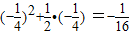 ,不满足不等式.
,不满足不等式.因此λ的范围就是 λ≤-1.
故答案为:(-∞,-1].
点评:本题考查函数恒成立问题的应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ≥0的解集为[-1,2)∪[3,+∞),则
≥0的解集为[-1,2)∪[3,+∞),则