题目内容
19（本小题满分14分）已知f(x)＝2x－1的反函数为
(x)，g(x)＝log4(3x＋1)．(1)若f－1(x)≤g(x)，求x的取值范围D；(2)设函数H(x)＝g(x)－(x)，当x∈D时，求函数H(x)的值域．
(Ⅰ) D＝[0，1] (Ⅱ) ［0，
］
解析:
：(Ⅰ)∵
∴
(x＞－1)
由
≤g(x) ∴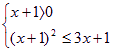
解得0≤x≤1 ∴D＝[0，1]
(Ⅱ)H(x)＝g(x)－
∵0≤x≤1 ∴1≤3－
≤2∴0≤H(x)≤ ∴H(x)的值域为［0，］
，函数
，
（其中
为自然对数的底数）．（1）求函数
在区间
上的最小值；（2）是否存在实数
，使曲线
在点
处的切线与
轴垂直? 若存在，求出
的值；若不存在，请说明理由．(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y( 码 ) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序 号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y( 码 ) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的
联列表:
| 高 个 | 非高个 | 合 计 | |
| 大 脚 | |||
| 非大脚 | 12 | ||
| 合 计 | 20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率；②抽到“无效序号(超过20号)”的概率.
是首项为19，公差为-4的等差数列，
为
项和.
及
是首项为1，公比为2的等比数列，求数列
的通项公式及其前
.
的左、右顶点分别为
，点P在椭圆上且异于
为坐标原点.
与
的斜率之积为
，求椭圆的离心率；
，证明：直线
的斜率
满足
.