题目内容
设直线![]() 是曲线
是曲线![]()
![]() 的一条切线,
的一条切线,![]() .
.
(Ⅰ)求切点坐标及![]() 的值;
的值;
(Ⅱ)当![]() 时,存在
时,存在![]()
![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅰ)解:设直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() , 解得
, 解得![]() 或
或![]() ,…………………………………2分
,…………………………………2分
当![]() 时,
时,![]() ,
,![]()
![]() 在曲线
在曲线![]() 上,∴
上,∴![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]() 在曲线
在曲线![]() 上,∴
上,∴![]() ,
,
切点![]() ,
,![]() , ……………………………………………4分
, ……………………………………………4分
切点![]() ,
, ![]() . ……………………………………………6分
. ……………………………………………6分
(Ⅱ)解法一:∵![]() ,∴
,∴![]() ,设
,设![]() ,若存在
,若存在![]()
![]() ,则只要
,则只要![]() , ……………8分
, ……………8分
![]() , (ⅰ)若
, (ⅰ)若![]() 即
即![]() ,令
,令![]() ,得
,得![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上是增函数,令
上是增函数,令![]() ,解得
,解得![]() ,
,![]()
![]() 在
在![]() 上是减函数,
上是减函数,![]()
![]() ,
,![]() ,解得
,解得![]() ,……………10分
,……………10分
(ⅱ)若![]() 即
即![]() ,令
,令![]() ,解得
,解得![]() ,
,![]() , ∴
, ∴![]() 在
在![]() 上是增函数,
上是增函数,![]()
![]()
![]() ,不等式无解,
,不等式无解,![]()
![]() 不存在,…11分
不存在,…11分
综合(ⅰ)(ⅱ)得,实数![]() 的取值范围为
的取值范围为![]() .………………………12分
.………………………12分
解法二:由![]() 得
得![]() , (ⅰ)当
, (ⅰ)当![]() 时,
时,![]() ,设
,设![]() 若存在
若存在![]()
![]() ,则只要
,则只要![]() ,…8分
,…8分![]() ,令
,令![]() 解得
解得![]()
![]()
![]() 在
在![]() 上是增函数,令
上是增函数,令![]() ,解得
,解得![]()
![]()
![]() 在
在![]() 上是减函数,
上是减函数,![]()
![]() ,
,![]()
![]() , ……………………10分
, ……………………10分
(ⅱ)当![]() 时,不等式
时,不等式![]() 不成立,∴
不成立,∴![]() 不存在, …………11分
不存在, …………11分
综合(ⅰ)(ⅱ)得,实数![]() 的取值范围为
的取值范围为![]() . ………12分
. ………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
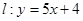 是曲线
是曲线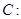
 的一条切线,
的一条切线, .
. 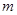 的值;
的值;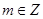 时,存在
时,存在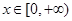
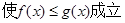 ,求实数
,求实数 的取值范围.
的取值范围.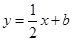 是曲线
是曲线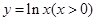 的一条切线,则实数
的一条切线,则实数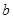 的值为
的值为 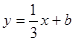 是曲线
是曲线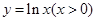 的一条切线,则实数
的一条切线,则实数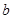 的值为
的值为 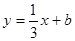 是曲线
是曲线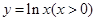 的一条切线,则实数
的一条切线,则实数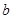 的值为
的值为