题目内容
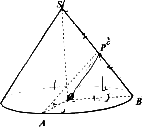
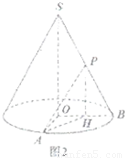
如图,已知圆锥体SO的侧面积为15π,底面半径OA和OB互相垂直,且OA=3,P是母线BS的中点.(1)求圆锥体的体积;
(2)异面直线SO与PA所成角的大小(结果用反三角函数表示).
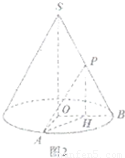
【答案】分析:(1)根据圆锥侧面积公式,结合题中数据列式,可得圆锥的母线长,再用勾股定理算出高的长度,最后用圆锥体积公式可得该圆锥的体积.
(2)取OB中点H,连接PH、AH,在△POB中,利用中位线定理,得到PH∥SO,故∠APH(或其补角)即为直线SO与PA所成角.在Rt△AOH中,计算出AH的长,最后在Rt△PAH中,利用正切的定义,得到异面直线SO与PA所成角的大小为arctan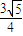 .
.
解答:解:(1)∵圆锥体SO的侧面积为15π,底面半径OA=3,
∴π•OA•SB=15π,得SB=5
Rt△SOB中,SO=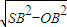 =4,即圆锥的高为4
=4,即圆锥的高为4
∴ 圆锥体的体积为V=
圆锥体的体积为V= π×32×4=12π
π×32×4=12π
(2)取OB中点H,连接PH、AH
∵△POB中,PH为中位线
∴PH∥SO,PH= SO=2
SO=2
故∠APH(或其补角)即为直线SO与PA所成角
∵SO⊥平面AOB,PH∥SO,
∴PH⊥平面AOB,可得PH⊥AH
∵△AOH中,AO⊥BO,HO= BO=
BO=
∴AH= =
=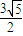
∴Rt△PAH中,tan∠APH=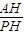 =
=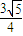 ,得∠APH=arctan
,得∠APH=arctan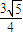 (锐角),
(锐角),
因此,异面直线SO与PA所成角的大小为arctan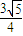 .
.
点评:本题给出圆锥一条母线的中点与底面圆上一点的连线,要我们求它与高线所成的角,着重考查了空间平行垂直的位置关系和异面直线所成角的求法,属于中档题.
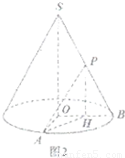
(2)取OB中点H,连接PH、AH,在△POB中,利用中位线定理,得到PH∥SO,故∠APH(或其补角)即为直线SO与PA所成角.在Rt△AOH中,计算出AH的长,最后在Rt△PAH中,利用正切的定义,得到异面直线SO与PA所成角的大小为arctan
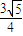 .
.解答:解:(1)∵圆锥体SO的侧面积为15π,底面半径OA=3,
∴π•OA•SB=15π,得SB=5
Rt△SOB中,SO=
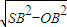 =4,即圆锥的高为4
=4,即圆锥的高为4∴
 圆锥体的体积为V=
圆锥体的体积为V= π×32×4=12π
π×32×4=12π(2)取OB中点H,连接PH、AH
∵△POB中,PH为中位线
∴PH∥SO,PH=
 SO=2
SO=2故∠APH(或其补角)即为直线SO与PA所成角
∵SO⊥平面AOB,PH∥SO,
∴PH⊥平面AOB,可得PH⊥AH
∵△AOH中,AO⊥BO,HO=
 BO=
BO=
∴AH=
 =
=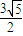
∴Rt△PAH中,tan∠APH=
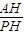 =
=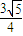 ,得∠APH=arctan
,得∠APH=arctan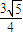 (锐角),
(锐角),因此,异面直线SO与PA所成角的大小为arctan
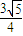 .
.点评:本题给出圆锥一条母线的中点与底面圆上一点的连线,要我们求它与高线所成的角,着重考查了空间平行垂直的位置关系和异面直线所成角的求法,属于中档题.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
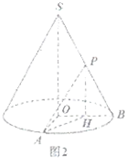 (2012•普陀区一模)如图,已知圆锥体SO的侧面积为15π,底面半径OA和OB互相垂直,且OA=3,P是母线BS的中点.
(2012•普陀区一模)如图,已知圆锥体SO的侧面积为15π,底面半径OA和OB互相垂直,且OA=3,P是母线BS的中点.