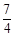题目内容
已知F是抛物线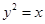 的焦点,A,B是该抛物线上的两点,
的焦点,A,B是该抛物线上的两点,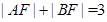 ,则线段AB的中点到y轴的距离为( )
,则线段AB的中点到y轴的距离为( )
A.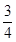 B.1 C.
B.1 C.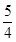 D.
D.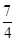
【答案】
C
【解析】
试题分析:∵F是抛物线y2=x的焦点
F(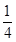 ,0)准线方程x=-
,0)准线方程x=-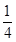 设A(x1,y1) B(x2,y2)
设A(x1,y1) B(x2,y2)
∴|AF|+|BF|=x1+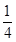 +x2+
+x2+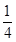 =3解得x1+x2=
=3解得x1+x2=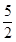 ∴线段AB的中点横坐标为
∴线段AB的中点横坐标为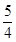 ∴线段AB的中点到y轴的距离为
∴线段AB的中点到y轴的距离为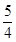 ,故选C.
,故选C.
考点:本题主要考查了解决抛物线上的点到焦点的距离问题,利用抛物线的定义将到焦点的距离转化为到准线的距离.
点评:解决该试题的关键是根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,求出线段AB的中点到y轴的距离.

练习册系列答案
相关题目
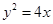 的焦点, A、B是抛物线上两点,若
的焦点, A、B是抛物线上两点,若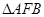 是正三角形,则
是正三角形,则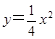 的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )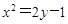 B.
B. C.
C.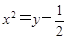 D.
D.
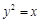 的焦点,A、B是该抛物线上的两点,
的焦点,A、B是该抛物线上的两点,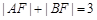 ,则线段AB的中点到y轴的距离为( )
,则线段AB的中点到y轴的距离为( )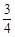 B.1 C.
B.1 C.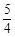 D.
D.