题目内容
19.甲、乙两袋装有大小相同的红球和白球,其中甲袋装有1个红球,4个白球;乙袋装有2个红球,3个白球.现从甲、乙两袋中各任取2个球.(Ⅰ)用ξ表示取到的4个球中红球的个数,求ξ的分布列及ξ的数学期望;
(Ⅱ)求取到的4个球中至少有2个红球的概率.
分析 (Ⅰ)由题意得ξ的所有可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(Ⅱ)取到的4个球中至少有2个红球的概率p=P(ξ≥2),由此能求出结果.
解答 解:(Ⅰ)由题意得ξ的所有可能取值为0,1,2,3,4,
P(ξ=0)=$\frac{{C}_{4}^{2}}{{C}_{3}^{2}}•\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{9}{50}$,
P(ξ=1)=$\frac{{C}_{4}^{1}}{{C}_{5}^{2}}•\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$+$\frac{{C}_{4}^{2}}{{C}_{5}^{2}}•\frac{{C}_{3}^{1}•{C}_{2}^{1}}{{C}_{5}^{2}}$=$\frac{12}{25}$,
P(ξ=2)=$\frac{{C}_{4}^{1}}{{C}_{5}^{2}}•\frac{{C}_{3}^{1}•{C}_{2}^{1}}{{C}_{5}^{2}}$+$\frac{{C}_{4}^{2}}{{C}_{5}^{2}}•\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$,
P(ξ=3)=$\frac{{C}_{4}^{1}}{{C}_{5}^{2}}•\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{25}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{9}{25}$ | $\frac{12}{25}$ | $\frac{3}{10}$ | $\frac{1}{25}$ |
(Ⅱ)由(Ⅰ)得取到的4个球中至少有2个红球的概率:
p=P(ξ≥2)=P(ξ=1)+P(ξ=2)=$\frac{3}{10}+\frac{1}{25}$=$\frac{17}{50}$.
点评 本题考查离散型随机变量的分布列、数学期望的求法,考查概率的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
7.对某电子元件进行寿命追踪调查,情况如下.
(1)画出频率分布直方图;
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
14.设函数f(x)可导,则$\lim_{△x→0}$$\frac{f(1+△x)-f(1)}{3△x}$等于( )
| A. | f′(1) | B. | 不存在 | C. | $\frac{1}{3}$f′(1) | D. | 以上都不对 |
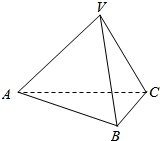 正三棱锥V-ABC的底面边长是a,侧面与底面成60°的二面角.求
正三棱锥V-ABC的底面边长是a,侧面与底面成60°的二面角.求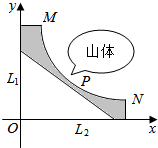 某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数).
某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数).