题目内容
若过椭圆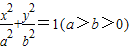 的焦点且垂直于x轴的直线被椭圆截得的弦长为a,则该椭圆的离心率为 .
的焦点且垂直于x轴的直线被椭圆截得的弦长为a,则该椭圆的离心率为 .
【答案】分析:根据题意,设过椭圆的右焦点且垂直于x轴的直线交椭圆于A、B两点,设A的坐标为(c,y),根据椭圆方程算出|y|=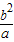 ,从而得到AB=
,从而得到AB=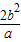 =a,可得a2=2b2,由此算出c=
=a,可得a2=2b2,由此算出c=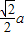 ,即可得到该椭圆的离心率.
,即可得到该椭圆的离心率.
解答:解:设过椭圆的右焦点且垂直于x轴的直线交椭圆于A、B两点,
可设A的坐标为(c,y),
∴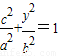 ,解之得y2=
,解之得y2=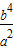 ,可得|y|=
,可得|y|=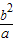
因此,AB=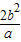 =a,可得a2=2b2,
=a,可得a2=2b2,
∴c=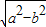 =
=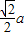 ,可得椭圆的离心率e=
,可得椭圆的离心率e=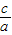 =
=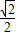
故答案为:
点评:本题给出椭圆的通径长等于它的半长轴a,求椭圆的离心率.着重考查了椭圆的标准方程与简单几何性质等知识点,属于基础题.
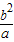 ,从而得到AB=
,从而得到AB=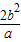 =a,可得a2=2b2,由此算出c=
=a,可得a2=2b2,由此算出c=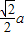 ,即可得到该椭圆的离心率.
,即可得到该椭圆的离心率.解答:解:设过椭圆的右焦点且垂直于x轴的直线交椭圆于A、B两点,
可设A的坐标为(c,y),
∴
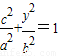 ,解之得y2=
,解之得y2=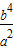 ,可得|y|=
,可得|y|=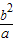
因此,AB=
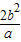 =a,可得a2=2b2,
=a,可得a2=2b2,∴c=
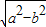 =
=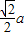 ,可得椭圆的离心率e=
,可得椭圆的离心率e=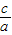 =
=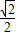
故答案为:

点评:本题给出椭圆的通径长等于它的半长轴a,求椭圆的离心率.着重考查了椭圆的标准方程与简单几何性质等知识点,属于基础题.

练习册系列答案
相关题目
 +
+ =1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1.
=1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1. 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.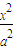 +
+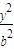 =1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1.
=1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1.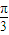 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.