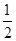题目内容
某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
A. | B. | C. | D. |
B
解析试题分析:三个电子元件的使用寿命均服从正态分布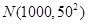 ,则三个电子元件的使用寿命超过1000小时的概率为
,则三个电子元件的使用寿命超过1000小时的概率为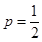 ,设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时,元件3正常},C={该部件的使用寿命超过1000小时},则
,设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时,元件3正常},C={该部件的使用寿命超过1000小时},则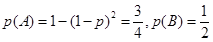 ,
,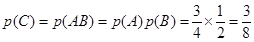 ,故答案选B.
,故答案选B.
考点:1.正态分布的知识;2.常见问题概率的求解.

练习册系列答案
相关题目
我校在模块考试中约有1000人参加考试,其数学考试成绩ξ~N(90,a2)(a>0,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生人数约为( )
,则此次数学考试成绩不低于110分的学生人数约为( )
| A.600 | B.400 | C.300 | D.200 |
某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是 ( )
| A.至多有一次中靶 | B.两次都不中靶 | C.两次都中靶 | D.只有一次中靶 |
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中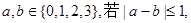 则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
A.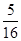 | B.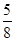 | C.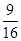 | D.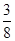 |
如果随机变量X~N(-1,σ2),且P(-3≤X≤-1)=0.4,则P(X≥1)等于( ).
| A.0.4 | B.0.3 | C.0.2 | D.0.1 |
 ,向正方形内随机地撒
,向正方形内随机地撒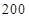 颗黄豆,数得落在阴影外的黄豆数为
颗黄豆,数得落在阴影外的黄豆数为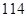 颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )
颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )





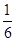 B.
B. 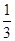 C.
C. 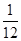 D.
D.