题目内容
已知抛物线C的顶点是坐标原点,对称轴是x轴,且点P(1,-2)在该抛物线上,A,B是该抛物线上的两个点.
(Ⅰ)求该抛物线的标准方程及焦点坐标;
(Ⅱ)若直线AB经过点M(4,0),证明:以线段AB为直径的圆恒过坐标原点;
(Ⅲ)若直线AB经过点N(0,4),且满足
=4
,求直线AB的方程.
(Ⅰ)求该抛物线的标准方程及焦点坐标;
(Ⅱ)若直线AB经过点M(4,0),证明:以线段AB为直径的圆恒过坐标原点;
(Ⅲ)若直线AB经过点N(0,4),且满足
| BN |
| AN |
分析:(Ⅰ)设抛物线C的标准方程为y2=2px,p>0.由点P(1,-2)在该抛物线上,能求出该抛物线的标准方程及焦点坐标.
(Ⅱ)设原点为O,A(x1,y1),B(x2,y2),AB直线方程为y=m(x-4),代入抛物线方程得:m2•(x-4)2=4x,m2x2-(8m2+4)x+16m2=0,利用韦达定理结合题设条件能够证明以线段AB为直径的圆恒过坐标原点.
(Ⅲ)A(x1,y1),B(x2,y2),由
=4
,得
=3
,即A为线段BN的定比分点,λ=3,由此能求出直线AB方程.
(Ⅱ)设原点为O,A(x1,y1),B(x2,y2),AB直线方程为y=m(x-4),代入抛物线方程得:m2•(x-4)2=4x,m2x2-(8m2+4)x+16m2=0,利用韦达定理结合题设条件能够证明以线段AB为直径的圆恒过坐标原点.
(Ⅲ)A(x1,y1),B(x2,y2),由
| BN |
| AN |
| BA |
| AN |
解答:解:(Ⅰ)∵抛物线C的顶点是坐标原点,对称轴是x轴,且点P(1,-2)在该抛物线上,
∴设抛物线C的标准方程为y2=2px,p>0.
∵点P(1,-2)在该抛物线上,
∴4=2p,解得p=2,
∴该抛物线的标准方程为y2=4x,焦点坐标为F(1,0).
(Ⅱ)设原点为O,A(x1,y1),B(x2,y2),AB直线方程为y=m(x-4),
代入抛物线方程得:m2•(x-4)2=4x,m2x2-(8m2+4)x+16m2=0,
则x1+x2=
,x1x2=16,
y1+y2=m(x1+x2-8)=
,
y1y2=m2(x1-4)(x2-4)=-16
AB2=(x1-x2)2+(y1-y2)2=(x1+x2)2-4x1x2+(y1+y2)2-4y1y2
=
-64+16-m2+64
=
,
OA2+OB2=x12+y12+x22+y22=(x1+x2)2-2x1x2+(y1+y2)2-2y1y2
=
-32+16-m2+32=
=AB2.
所以,以线段AB为直径的圆恒过坐标原点.
(Ⅲ)A(x1,y1),B(x2,y2),
由
=4
,得
=3
,
即A为线段BN的定比分点,λ=3,
∴x1=
,y1=
,
∵y22=4x2,①
(
)2=4x1=x2,②
解得x2=4,y2=-4,
∴B(4,-4),
∵AB过N(0,4),
∴直线AB方程:
=
,即 2x+y-4=0.
∴设抛物线C的标准方程为y2=2px,p>0.
∵点P(1,-2)在该抛物线上,
∴4=2p,解得p=2,
∴该抛物线的标准方程为y2=4x,焦点坐标为F(1,0).
(Ⅱ)设原点为O,A(x1,y1),B(x2,y2),AB直线方程为y=m(x-4),
代入抛物线方程得:m2•(x-4)2=4x,m2x2-(8m2+4)x+16m2=0,
则x1+x2=
| 8m2+4 |
| m2 |
y1+y2=m(x1+x2-8)=
| 4 |
| m |
y1y2=m2(x1-4)(x2-4)=-16
AB2=(x1-x2)2+(y1-y2)2=(x1+x2)2-4x1x2+(y1+y2)2-4y1y2
=
| (8m2+4)2 |
| m4 |
=
| 80m4+64m2+16 |
| m4 |
OA2+OB2=x12+y12+x22+y22=(x1+x2)2-2x1x2+(y1+y2)2-2y1y2
=
| (8m2+4)2 |
| m4 |
| 80m4+64m2+16 |
| m4 |
所以,以线段AB为直径的圆恒过坐标原点.
(Ⅲ)A(x1,y1),B(x2,y2),
由
| BN |
| AN |
| BA |
| AN |
即A为线段BN的定比分点,λ=3,
∴x1=
| x2 |
| 4 |
| y2+12 |
| 4 |
∵y22=4x2,①
(
| y2+12 |
| 4 |
解得x2=4,y2=-4,
∴B(4,-4),
∵AB过N(0,4),
∴直线AB方程:
| y-4 |
| x |
| -4-4 |
| 4 |
点评:本题考查抛物线标准方程和焦点坐标的求法,考查圆恒过定点的证明,考查直线方程的求法.解题时要注意向量知识和韦达定理的合理运用.

练习册系列答案
相关题目
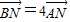 ,求直线AB的方程.
,求直线AB的方程.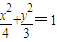 的中心,且焦点与该椭圆右焦点重合.
的中心,且焦点与该椭圆右焦点重合.