题目内容
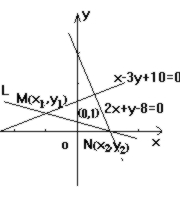
若直线l与直线x - 3y + 10 = 0, 2x + y - 8 = 0分别交于M、N, 若线段MN的中点为(0,1)那么直线l的方程为[ ]
A. x + 4y - 4 = 0 B. 4x + y - 4 = 0
C. x - 4y + 4 = 0 D. x - 4y - 4 = 0
答案:A
解析:
提示:
解析:
|
解: 设点M、N的坐标分别为(x1,y1), (x2,y2) 所以 x1+ x2 = 0 y1+ y2 = 2 ① 但 x1- 3y1+ 10 = 0 2x2+ y2 - 8 = 0 即 2(x1+ x2) - 6y1+ y2- 6 = 0 y2-6y1+ 12 = 0 ② ①代入② -7y1= -14, y1= 2, y2= 2- y1 = 0 x1= -4, x2= 4
又 因为 kMN =
所以 y - 1 = -
|
提示:
| 设点M、N的坐标为(x1,y1),(x2,y2), 利用中点坐标求x1, y1和x2, y2,再求kMN就可得所求的方程. |

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
若直线l与直线x-3y+10=0交于点M,与直线2x+y-8=0交于点N,MN的中点为P(0,1),则直线l的方程是( )
| A、x+4y+4=0 | B、x+4y-4=0 | C、x-4y+4=0 | D、x-4y-4=0 |