题目内容
已知半径为
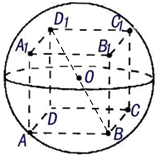
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
| 3 |
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
分析:(1)根据球的体积公式加以计算,可得此球的体积;
(2)由正方体的性质可得正方体的对角线长等于它的外接球直径,由此利用正方体对角线公式,算出正方体的棱长为2,可得球的内接正方体的体积;
(3)根据前面算出的数据,利用球的表面积公式与正方体的全面积公式加以计算,可得所求的面积之比.
(2)由正方体的性质可得正方体的对角线长等于它的外接球直径,由此利用正方体对角线公式,算出正方体的棱长为2,可得球的内接正方体的体积;
(3)根据前面算出的数据,利用球的表面积公式与正方体的全面积公式加以计算,可得所求的面积之比.
解答:解:(1)∵球的半径为R=
,
∴球的体积为V=
πR3=
π×(
)3=4
π;
(2)设正方体的棱长为a,可得正方体的对角线长为
a,
∵球的半径为
,且正方体内接于球,
∴正方体的对角线就是球的直径,可得
a=2
,解得a=2.
因此,此球的内接正方体的体积V1=a3=23=8;
(3)由(2)得内接正方体的棱长a=2,可得正方体的全面积为S1=6a2=24.
又∵球的表面积S2=4πR2=12π,
∴此球的表面积与其内接正方体的全面积之比为
=
=
.
| 3 |

∴球的体积为V=
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
(2)设正方体的棱长为a,可得正方体的对角线长为
| 3 |
∵球的半径为
| 3 |
∴正方体的对角线就是球的直径,可得
| 3 |
| 3 |
因此,此球的内接正方体的体积V1=a3=23=8;
(3)由(2)得内接正方体的棱长a=2,可得正方体的全面积为S1=6a2=24.
又∵球的表面积S2=4πR2=12π,
∴此球的表面积与其内接正方体的全面积之比为
| S2 |
| S1 |
| 12π |
| 24 |
| π |
| 2 |
点评:本题给出球的内接正方体,在已知球的半径的情况下求正方体的体积与表面积.着重考查了正方体的性质、球的体积与表面积计算和球内接多面体等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
