题目内容
若函数![]() 对任意的实数
对任意的实数![]() ,
,![]() ,均有
,均有![]() ,则称函数
,则称函数
![]() 是区间
是区间![]() 上的“平缓函数”.
上的“平缓函数”.
(1) 判断![]() 和
和![]() 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;
(2) 若数列![]() 对所有的正整数
对所有的正整数![]() 都有
都有 ![]() ,设
,设![]() ,
,
求证: ![]() .
.
 当
当![]() 时,同理有
时,同理有![]() 成立
成立
又当![]() 时,不等式
时,不等式![]() ,
,
故对任意的实数![]() ,
,![]() R,均有
R,均有![]() .
.
因此 ![]() 是R上的“平缓函数”. …………… 5分
是R上的“平缓函数”. …………… 5分
由于![]() …………… 6分
…………… 6分
取![]() ,
,![]() ,则
,则![]() , …………… 7分
, …………… 7分
因此, ![]() 不是区间R的“平缓函数”. …………… 8分
不是区间R的“平缓函数”. …………… 8分


练习册系列答案
相关题目
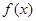 对任意的实数
对任意的实数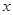 都有
都有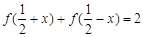 成立,则
成立,则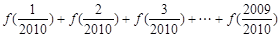 =
.
=
.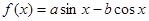 对任意的实数
对任意的实数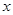 都有
都有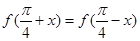 ,则
,则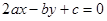 的斜率是( )
的斜率是( )