题目内容
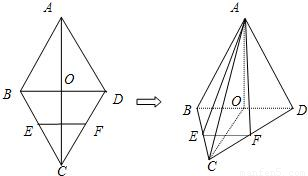
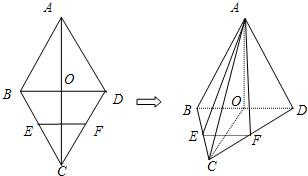 已知菱形ABCD的两条对角线交于点O,且AC=8,BD=4,E、F分别是BC、CD的中点,将△ABD沿BD折起,使平面ABD⊥平面BDC、
已知菱形ABCD的两条对角线交于点O,且AC=8,BD=4,E、F分别是BC、CD的中点,将△ABD沿BD折起,使平面ABD⊥平面BDC、(1)求证EF⊥平面AOC;
(2)求AE与平面AOC所成角的正弦值;
(3)求点B到平面AEF的距离.
分析:(1)欲证EF⊥平面AOC,而EF∥BD,可先证BD⊥平面AOC,而BD⊥AO,BD⊥OC,AO∩OC=O满足定理条件;
(2)设EF与交于点G,连接AG,根据线面所成角的定义可知∠EAG是AE与平面AOC所成的角,在三角形EAG中求出此角的正弦值即可;
(3)点B到平面AEF的距离等于点O到平面AEF的距离,而点O到平面AEF的距离点等于点O到AG的距离,在△AOG中即可求出点B到平面AEF的距离.
(2)设EF与交于点G,连接AG,根据线面所成角的定义可知∠EAG是AE与平面AOC所成的角,在三角形EAG中求出此角的正弦值即可;
(3)点B到平面AEF的距离等于点O到平面AEF的距离,而点O到平面AEF的距离点等于点O到AG的距离,在△AOG中即可求出点B到平面AEF的距离.
解答:解:(1)证:由BD⊥AO,BD⊥OC,得BD⊥平面AOC,
又E,F分别为BC,CD的中点,EF∥BD,
所以,EF⊥平面AOC.(4分)
(2)设EF与交于点G,连接AG.由(1)EF⊥平面AOC,
得AE与平面AOC所成的角为∠EAG.(6分)
AG=2
,EG=1,AE=
,sin∠EAG=
,
所以,AE与平面AOC所成角的正弦值为
.(8分)
(3)由EF∥BD,得BD∥平面AEF,
所以,点B到平面AEF的距离等于点O到平面AEF的距离
又EF⊥平面AOC,EF?平面AEF,得平面AOC⊥平面AEF,
所以,点O到平面AEF的距离点等于点O到AG的距离.(10分)
在△AOG中,AO=4,OG=2,AG=2
,
所以,点B到平面AEF的距离为
.(12分)
又E,F分别为BC,CD的中点,EF∥BD,
所以,EF⊥平面AOC.(4分)
(2)设EF与交于点G,连接AG.由(1)EF⊥平面AOC,
得AE与平面AOC所成的角为∠EAG.(6分)
AG=2
| 5 |
| 21 |
| ||
| 21 |
所以,AE与平面AOC所成角的正弦值为
| ||
| 21 |
(3)由EF∥BD,得BD∥平面AEF,
所以,点B到平面AEF的距离等于点O到平面AEF的距离
又EF⊥平面AOC,EF?平面AEF,得平面AOC⊥平面AEF,
所以,点O到平面AEF的距离点等于点O到AG的距离.(10分)
在△AOG中,AO=4,OG=2,AG=2
| 5 |
所以,点B到平面AEF的距离为
4
| ||
| 5 |
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角和点到面的距离,属于基础题.

练习册系列答案
相关题目
 =-1-i,
=-1-i, ,点C对应的复数
,点C对应的复数 的辐角主值为
的辐角主值为 ,求点D所对应的复数.
,求点D所对应的复数.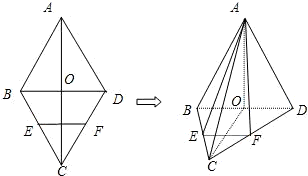 已知菱形ABCD的两条对角线交于点O,且AC=8,BD=4,E、F分别是BC、CD的中点,将△ABD沿BD折起,使平面ABD⊥平面BDC、
已知菱形ABCD的两条对角线交于点O,且AC=8,BD=4,E、F分别是BC、CD的中点,将△ABD沿BD折起,使平面ABD⊥平面BDC、