题目内容
“1＜a＜2”是“对任意的正数x，2x+
≥2”成立的（ ）A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】分析：已知“对任意的正数x，2x+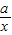
≥2”利用均值不等式，求出a的范围，再根据充分必要的定义进行判断；
解答：解：“对任意的正数x，2x+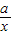
≥2”，
可得2x+
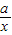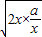≥2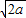
=2
≥2，
∴
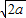≥1，解得a
，
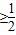若“1＜a＜2”可得2x+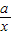
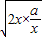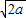≥2
=2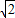
＞2
＞2，
∴“1＜a＜2”⇒“对任意的正数x，2x+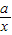
≥2”，
∴“1＜a＜2”是“对任意的正数x，2x+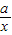
≥2”成立的充分不必要条件，
故选A；
点评：此题主要考查均值不等式的应用，以及充分必要条件的定义，是一道基础题；
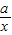≥2”利用均值不等式，求出a的范围，再根据充分必要的定义进行判断；解答：解：“对任意的正数x，2x+
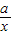≥2”，可得2x+
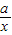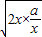≥2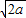=2≥2，∴
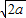≥1，解得a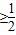，若“1＜a＜2”可得2x+
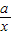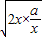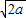≥2=2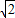＞2＞2，∴“1＜a＜2”⇒“对任意的正数x，2x+
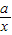≥2”，∴“1＜a＜2”是“对任意的正数x，2x+
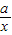≥2”成立的充分不必要条件，故选A；
点评：此题主要考查均值不等式的应用，以及充分必要条件的定义，是一道基础题；
练习册系列答案
相关题目
2”的
的（ ）