题目内容
设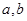 为正实数,现有下列命题:
为正实数,现有下列命题:
①若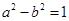 ,则
,则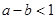 ;
;
②若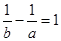 ,则
,则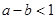 ;
;
③若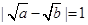 ,则
,则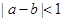 ;
;
④若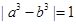 ,则
,则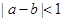 .
.
其中的真命题有____________.(写出所有真命题的编号)
①④
解析试题分析:①若a2-b2=1,则a2-1=b2,即(a+1)(a-1)=b2,∵a+1>a-1,∴a-1<b,即a-b<1,①正确;
②若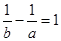 ,可取a=7,b=
,可取a=7,b= ,则a-b>1,∴②错误;
,则a-b>1,∴②错误;
③若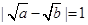 ,则可取a=9,b=4,而|a-b|=5>1,∴③错误;
,则可取a=9,b=4,而|a-b|=5>1,∴③错误;
④由|a3-b3|=1,
若a>b,则a3-b3=1,即a3-1=b3,即(a-1)(a2+1+a)=b3,∵a2+1+a>b2,∴a-1<b,即a-b<1;
若a<b,则b3-a3=1,即b3-1=a3,即(b-1)(b2+1+b)=a3,∵b2+1+b>a2,∴b-1<a,即b-a<1;
∴|a-b|<1∴④正确;
故答案为①④
考点:不等式的性质
点评:中档题,可通过举反例的方法证明某些命题的错误性。要想说明命题正确,应给出严格的证明。

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
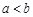 ,则
,则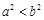 ;
;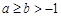 ,则
,则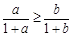 ;
;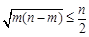 ;
; 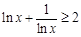 .
.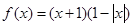 的图像恒在
的图像恒在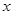 轴上方,则
轴上方,则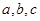 满足
满足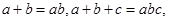 则
则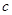 的取值范围是 .
的取值范围是 .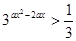 对一切实数
对一切实数 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .



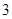


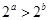
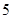
 中,你认为正确的是 .(填序号).
中,你认为正确的是 .(填序号). 都成立的一组值(a、b、c、d)是 。(只要写出适合条件的一组值即可)
都成立的一组值(a、b、c、d)是 。(只要写出适合条件的一组值即可)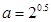 ,
,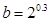 ,
, ,则
,则 的大小关系为 (用符号“<”连接)
的大小关系为 (用符号“<”连接) ,使等式
,使等式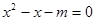 成立”是真命题.
成立”是真命题.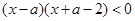 的解集为N,若
的解集为N,若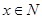 是
是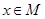 的必要条件,求a的取值范围.
的必要条件,求a的取值范围.