题目内容
在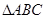 中,内角
中,内角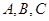 的对边分别为
的对边分别为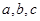 . 已知
. 已知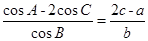 .
.
(1)求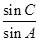 的值; (2) 若
的值; (2) 若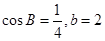 ,求
,求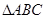 的面积.
的面积.
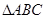 中,内角
中,内角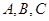 的对边分别为
的对边分别为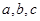 . 已知
. 已知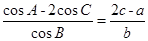 .
.(1)求
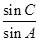 的值; (2) 若
的值; (2) 若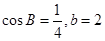 ,求
,求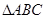 的面积.
的面积. (1)
(1) ,(2)
,(2) .
.试题分析:(1)要求角的关系,所以要用正弦定理,
 即
即 ,再用积化和差公式,化为
,再用积化和差公式,化为 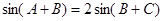 ,有因为
,有因为 ,得到
,得到 .
.(2) 在解三角形中求面积一般用
 ,给出了角
,给出了角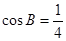 ,所以本题关键是求
,所以本题关键是求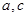 的值.由(1)中给出了
的值.由(1)中给出了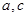 之间的关系,且
之间的关系,且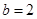 所以由余弦定理就可解除
所以由余弦定理就可解除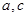 ,进而本题得解.
,进而本题得解.试题解析:(1)由正弦定理知

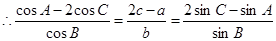 ,即
,即 ,化为
,化为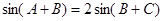 ,得
,得 ,所以
,所以 .
.(2)由(1)知
 ,即
,即 ,又因为
,又因为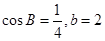 ,所以由余弦定理
,所以由余弦定理  得
得 ,解得
,解得 ,因为
,因为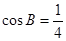 ,所以
,所以 ,故
,故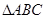 的面积为
的面积为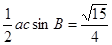 .
.
练习册系列答案
相关题目
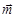 =(sinA,1),
=(sinA,1),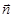 =(cosA,
=(cosA,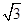 ),且
),且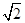 ,求△ABC的面积.
,求△ABC的面积.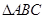 中,角
中,角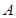 、
、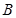 、
、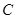 的对边分别为
的对边分别为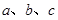 ,且
,且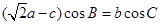 .
. ,且
,且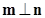 ,求
,求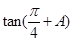 的值.
的值.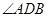 =750,
=750,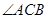 ="30°,AD" =
="30°,AD" =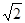 .
.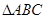 中,
中,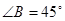 ,
, 是
是 边上一点,
边上一点, ,则
,则 的长为 .
的长为 .
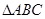 的内角
的内角 所对的边分别为
所对的边分别为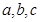 ,已知
,已知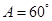 ,
,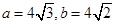 ,则角
,则角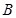 的大小为
的大小为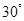
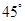
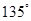
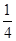 B.
B.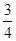 C.
C.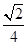 D.
D.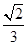
 ,A、B、C成等差数列,则角C=( )
,A、B、C成等差数列,则角C=( ) B.
B. C.
C.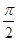 D.
D.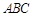 中,
中,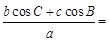 .
.